Proszę o rozwiązanie tych zadanek. Schrodinger: 1. Wiedząc że sinαcosα=0.4 oblicz sinα−cosα .

	√3
2. Rozwiąż równanie |sin3x|=		, x∊<0,π>
	2

3. Sprawdź tożsamość trygonometryczną:

	sinx		1
a. ctgx +		=
	1−cosx		sinx

	sinx		1+cosx		2
b.		+		=
	1+cosx		sinx		sinx

	π
4. Rozwiąż równanie: sin(x +		)
	6

Schrodinger: Nie dokończyłem pisać zadań i przypadkowo kliknąłem opublikuj.

	π		π
równanie w 4 powinno wyglądać tak : sin(x +		) * sin(x −		= 0.5, x∊<0,2π>
	6		6

5. Narysuj wykres funkcji f(x)= 2|sinx|cosx gdzie x∊<−2π,2π>, wyznacz wszustkie wartości parametru x dla których f(x)=1. Z góry dziękuję za pomoc ale proszę tylko o rozwiązywanie zadań a nie ich tłumaczenie.

PuRXUTM: a może coś sam zaczniesz ? Napisz do czego doszedłeś

Schrodinger: Bardzo potrzebuje tylko rozwiązań tych zadań więc jeśli znajdzie się jakaś dobra dusza która spełni moją potrzebę będę bardzo wdzięczny.

PuRXUTM: tylko byśmy Ci zaszkodzili... nauka matematyki bez zrozumienia istoty zadania nie ma najmniejszego sensu...

wredulus_pospolitus: haha ... każdy potrzebuję (baaardzo potrzebuje) rozwiązań a TYLKO rozwiązań to potrzebuje ktoś kto się obudził z ręką w nocniku, że jak nie odda pracy domowej to go w szkole nie dopuszczą do matury ... obleje rok ... czy coś innego − rodzice się dowiedzą i będzie co będzie

Schrodinger: To są pytania ze sprawdzianu który opuściłem. Pisząc go w 2 terminie i tak dostanę inne pytania lecz chciałem zobaczyć metody rozwiązywania tego typu zadań aby zwyczajnie sobie je przypomnień. Wasza pomoc teoretycznie jest mi zbędna lecz nic wielkiego by się nie stało jeśli spełnilibyście moją prośbę, podsumowując wasze odpowiedzi okazały się niezmiernie pomocne.

Schrodinger: Przypomnieć*

PW: 1. Wskazówka: (sinx−cosx)² = sin²x+cos²x+2sinxcosx. Kwadrat zadanego wyrażenia mamy. Tyle że odpowiedzi wtedy mogą być dwie − dodatnia i ujemna. Obie dobre, czy tylko jedna?

PW: Diabli z tym "plusem−minusem" na jednym klawiszu. Oczywiście powinno byc −2sinxcosx.

wredulus_pospolitus: PW ..ekhm ... tam nie − ... tylko + w nawiasie winien być

PW: Żartuj sobie ze starego ślepnącego człowieka.

Schrodinger: Byłbym bardzo wdzięczny za wskazówki do zadania 2 i 5 ponieważ to ona sprawiają mi największe problemy.

PW: Nie nabieraj nas. Zadania 5. nie ma (tyle jeszcze widzę). Wskazówka do zadania 2.

	√3		√3		√3
|a| =		⇔ a =		∨ a = −		,
	2		2		2

są więc do rozwiązania dwa proste równania. Oba mają rozwiązania, gdyż jeśli x∊[0, π], to 3x∊[0, 3π]. Warto to narysować.

Schrodinger: Zadanie 5. jest w 2 od góry poście .

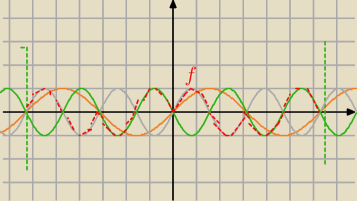
Aga1.: 5) f(x)=2sinxcosx=sin2x dla sinx≥0 (y=sin2x kolor szary) f(x)=−2sinxcosx=−sin2x, gdy sinx<0 (y=−2sinx kolor zielony) (y=sinx kolor pomarańczowy)

PW: Pora umierać 5. Narysuj wykres funkcji f(x)= 2|sinx|cosx gdzie x∊<−2π,2π>, wyznacz wszystkie wartości parametru x dla których f(x)=1. Tam gdzie sinx≥0 mamy funkcję 2sinxcosx=sin2x, a tam gdzie sinx <0 mamy f(x) = −sin2x. Rysujemy sinx na [−2π, 2π] − z tego odczytujemy gdzie sinx ≥ 0.

	⎧	sin2x dla x∊...
f(x) =	⎨		.
	⎩	−sin2x dla ...

Rysunek polega więc na narysowaniu sin2x lub (−sin2x) na odpowiednich przedziałach.

Schrodinger: Dziękuję bardzo za pomoc. c: