f. kwadratowa
Sad: znajdz te wartosci parametru m dla ktorych funkcja f(x)=x2 +mx +9 ma dwa miejsca zerowe
wieksze od 2
10 lut 16:44
J:
1) yw < 0
2) xw > 2
3) f(2) < 0
10 lut 16:50
J: Ad 3) Oczywiście f(2) > 0
10 lut 16:56
Sad: mam to liczyć deltą?
10 lut 16:59
J: Nie musisz.Warunek 1) gwarantuje istnienie 2 −ch pierwiastków i Δ > 0
10 lut 17:00
Sad: więc co powinnam teraz zrobić?
10 lut 17:02
J: | | Δ | |
No tak, jednak musisz policzyć Δ , bo yw = − |
| |
| | 4 | |
10 lut 17:06
Sad: Δ=m2−36
m2−36=0
Δ=144m2
x1=−12m/2=−6m
x2=12m/2=6m
−6m>2 6m>2
m<−3 m>3
10 lut 17:09
Marcin: Jak widzisz, że funkcja ma mieć dwa miejsca zerowe, lub ew jedno, to bez zastanowienia licz Δ
10 lut 17:09
Sad: m∊(−∞,−3) u (3,∞)
to jest koniec?
10 lut 17:11
J: | | −(m2−36) | |
1) yw < 0 ⇔ |
| <0 ⇔ m2 − 36 > 0 ⇔ m2 > 36 ⇔ ... |
| | 4 | |
10 lut 17:15
Sad:
m
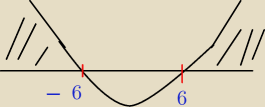
2−36>0
(m−6)(m+6)>0
m∊(−
∞,−6) u (6,
∞)
10 lut 17:29
J: | | m | |
Teraz warunek 2) : xw > 2 czyli − |
| > 2 |
| | 2 | |
10 lut 17:33
Sad: z 1) mamy m∊(−∞,−6) u (6,∞)
z 2) mamy m<4
3) f(2)>0
4+2m+9>0
m>−11/2
ost. m∊(−11/2,−6)
10 lut 17:40
J: Policz jeszcze raz 3)
10 lut 17:43
Sad: z 3) mamy m>−13/2
ost. m∊(−13/2,−6)
10 lut 17:44
J: Tak.
10 lut 17:45
Sad: dzięki za pomoc
10 lut 17:45