bryły bezendu: Krawędź boczna ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta między sąsiednimi ścianami bocznymi.

	1
cosα=−
	15

Proszę o sprawdzenie

wredulus_pospolitus:

	15		15		15
2 =		+		− 2*		cosα
	4		4		4

	11		4		11
cosα =		*		=
	4		15		15

chyba że sie pomyliłem w obliczeniach (w głowie)

	√15
hściany bocznej =		a ; a −−− krawędź podstawy
	2

d_podstawy = √2a

bezendu: wredulus. ja mam tak

	√15a		√15a		√15a		√15a
(a√2)2=(		)2+(		)2−2*		*		*cosα
	4		4		4		4

16a²=15a²−15a²cosα a²=−15a²cosα

	−1
cosα=
	15

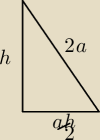wredulus_pospolitus: no to masz źle h_{sciany bocznej}

	a2		15		√15
h2 +		= 4a2 −> h2 =		a2 −> h =
	4		4		2

zauważ, że Ci wyszło: h<1*a a/2 < 1*a więc: h+ a/2 < a+a = 2a hmmm

bezendu:

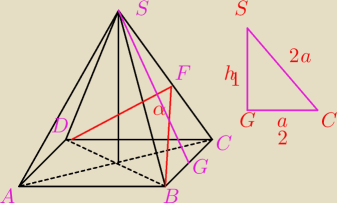
	a
h12=(2a)2−(		)2
	2

	a2
h12=4a2−
	4

	15a2
h12=
	4

	√15a
h1=
	2

	1		√15a
PΔBSC=		*a*
	2		2

	√15a2
PΔBSC=
	4

1		√15a2
	*|BF|*2a=
2		4

	√15a
BF=
	4

I dalej tak jak w poprzednim moim poście

Saizou :

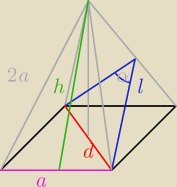
	1
h2+(		a)2=(2a)2
	2

	1
h2+		a2=4a2
	4

	15
h2=		a2
	4

	√15
h=		a
	2

1		√15		1
	a*		a =		l*2a
2		2		2

√15a=4l

	√15
l=		a
	4

d=a√2

	√15		√15
(a√2)2=2(		a)2−2(		a)2*cosα
	4		4

	15		15
2a2=2*		a2−2		a2*cosα /2a2
	16		16

	15		15
1=		−		*cosα
	16		16

1		15
	=−		cosα
16		16

	1
cosα=−
	15

bezendu: Saizou liczyłem tak jak Ty. Dzięki Panowie

Saizou : no i gites

wredulus_pospolitus: brrr ... liczyłem cosinusa dla przeciwległych ścian a tego to już w ogóle by mi się nie chciało liczyć