Najmniejsza największa wartość w przedziale alina: Proszę o pomoc wyznacz najmniejszą największą wartość funkcji y=−x+32/(x²) w przedziale domkniętym [1;6]

zawodus: funkcja wygląda tak?

	32
f(x)=−x+
	x2

alina: pomoże ktoś

Bizon: ile jeszcze można ?

	−x+32		32
y=		czy y=−x+
	x2		x2

alina: tak

alina: y= −x+³²_x²

Bizon: ... licz pochodną ... przyrównuj do 0 i analizuj −

PW: Obliczamy f(1) oraz f(6) − wartości na krańcach zadanego przedziału. Byłyby to ekstrema, gdyby funkcja zachowywała się "grzecznie" na tym przedziale (rosła lub malała). Liczymy więc pochodną funkcji, żeby to zbadać. Jeżeli okaże się, że f ma ekstremum lokalne w punkcie x₀∊[1, 6], to rozstrzygamy między f(1), f(x₀), f(6).

alina: pochodna to −1−64/x³

alina: policzyłam na krańcach otrzymałam 31 i −5 1/9

5-latek:

	64
czy aby napewno (U{32}{x2)'= −		?
	x3

5-latek:

	0*x2−32*2x		64
=		=−		wiec tyle sie rowna
	x4		x3

5-latek: Ale nie gniewaj sie na mnie za to

alina: wydaje mi się♣ że nie masza racji pochodna z −x+³²_x² to na pewno −1−64/x³

5-latek:

	32
Tak wiem ale ja tylko policzylem (		)'
	x2

5-latek:

	64
1−		=0 /*(x3)
	x3

x³−64=0 to (x−4)(x²+4x+16)=0 to (x−4)=0 lub x²+4x+16=0 ale dalej juz sama

5-latek:

	64
Przepraszam na byc −1−		=0
	x3

to bedzie −x³−64=0 dalej kombinuj

wredulus_pospolitus: ale co tu kombinować: x³ = −64 x = −³√64 = −³√2⁶ = −2² = −4

5-latek: Artur . Chcialem ze zeby to ze wzoru skroconego mnozenia rozwalila nasza kolezanka

Janek191: y' = − 1 − U{64}[x³} Dla x > 0 jest y' < 0 więc funkcja maleje w całym < 1; 6 > czyli y_max = f(1) y_min = f(6)

Janek191: y' = − 1 − U{64}[x³} Dla x > 0 jest y' < 0 więc funkcja maleje w całym < 1; 6 > czyli y_max = f(1) y_min = f(6)

Janek191:

	64
Miało być y' = − 1 −
	x3

Janek191:

	64
Miało być y' = − 1 −
	x3

5-latek: A Alina pewnie juz po kolokwium

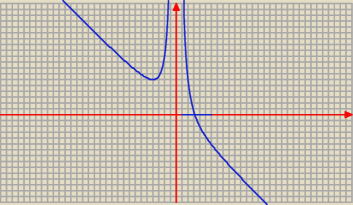
Janek191: Fajnie widać na wykresie

Janek191: Może się odezwie

5-latek: Miejmy taka nadzieje

alina: dziękuje bardzo