1ehh qu: Podobno trudne Prostokąt o bokach długości 16 i 12 obraca się wokół przekątnej. Oblicz objętość otrzymanej bryły obrotowej 4269/5π− odp

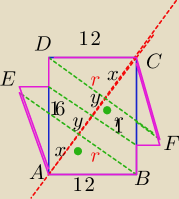
Janek191: I AC I² = 12² + 16² = 144 + 256 = 400 I AC I = 20 P_ΔABC = 0,5*12*16 = 96 oraz 0,5 *I AC I*r = P_ΔABC = 96 0,5*20*r = 96 10 r = 9,6 r = 9,6 −−−−− oraz x² + r² = 12² x² + 9,6² = 144 x² = 144 − 92,16 = 51,84 x = 7,2 −−−−−−− 2y = 20 − 2x = 20 − 2*7,2 = 20 − 14,4 = 5,6 y = 2,8 −−−−−−

r		x + 2y
	=
r1		x + y

9,6		12.8
	=
r1		10

r₁ = 7,5 −−−−−−−− Objętość bryły obrotowej :

	1		1
V = 2*		π r2*x + 2*		π*( r2 + r*r1 + r12)*y =
	3		3

	2		2
=		π *92,16*7,2 +		π*(9,62 + 9,6*7,5 + 7,52)*2,8 =
	3		3

	2
= 442,368 π +		π*(92,16 + 72 + 56,25)*2,8 = 442,368 π + 411,432 π = 853,8 π
	3

====================================================================

zawodus: Fajne zadanko

2: W środku są dwa ścięte stożki ?

Janek191: Tak

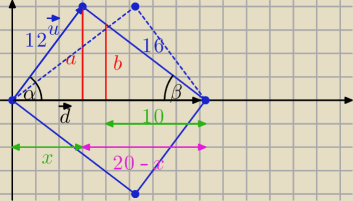Trivial: Inny sposób rozwiązania. Wyznaczamy długość przekątnej: ||d|| = √12² + 16² = 20. Można zauważyć symetrię wzdłuż prostej poprowadzonej przez odcinek b, a zatem objętość będzie: V = 2*¹₃π(xa² + (20−x)a² − 10b²) = ²⁰₃π(2a² − b²) Zatem wystarczy wyznaczyć a oraz b. Korzystając z rachunku wektorowego wyznaczamy cosα

	u∘d		(0,12)∘(16,12)		12*12		3
cosα =		=		=		=
	||u||*||d||		12*20		12*20		5

	4
sinα = √1−cos2α =
	5

a = 12*sinα = 9.6 Zauważamy, że α+β = 90^o → β = 90^o−α czyli:

	sin(90o−α)		cosα		3
tanβ =		=		=
	cos(90o−α)		sinα		4

b = 10*tanβ = 7.5 Zatem V = ²⁰₃π(184.32 − 56.25) = 853.8π