Wyznacz punkty z wykresu x^2 leżące najbliżej punktu P=(0,2) Norbi: Wyznacz punkty z wykresu x² leżące najbliżej punktu P=(0,2)

Ada: A=(x,x²) − punkt leżący na paraboli f(x)=d²=(x−0)²+(x²−2)² − funkcja opisująca kwadrat odległości dowolnego punku na paraboli od punktu P Znajdź jej minimum.

Norbi: Dzięki

Norbi: Wyszły mi 3 punkty : (0,0) (3/2,9/4) (−3/2,9/4) czy ktoś może zweryfikować moją odpowiedź ?

...: ... jak widzisz NIE

AS: Odp. x = ±√3/2, x = 0

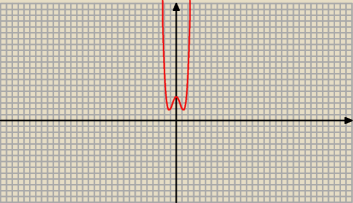
Janek191: Wykres funkcji f (x) = x⁴ − 3 x² + 4 bo d² = f(x) =( x − 0)² + ( x² − 2)² = x² + x⁴ − 4 x² + 4 = x⁴ − 3 x² + 4

	√6		√6
f '(x) = 4 x3 − 6 x = 2x*( 2 x2 − 3) = 0 ⇔ x = 0 lub x = −		lub x =
	2		2

Minima lokalne dla x = − 0,6√6 i x = 0,5√6 zatem szukane punkty, to A₁ = ( − 0,5√6 ; 1,5) , A₂ = ( 0,5√6; 1,5 ) ======================================

Janek191: Pomyłka minima dla x = − 0,5√6 i x = 0,5√6

AS: U mnierównież , odpada przypadek x= 0

Bizon: x=0 odpada, bo analizując pochodną x=0 nie spełnia drugiego warunku Chcąc się "przyczepić" do rozwiązania Janka191 można by rzec, ze analizował funkcję d²=... a nie d=.... bez stosownego stwierdzenia −