1
qu: jaką wysokość powinien mieć ostrosłup prawidłowy czworokątny o krawędzi bocznej 10√3, aby
jego objętość była największa
9 lut 23:27
qu: wychodzi mi coś dziwnego
−h3 − 300h = V
muszę to zrobić bez pochodnych
9 lut 23:47
qu: jest ktoś w stanie pomóc ?
przynajmniej jakaś wskazówka
9 lut 23:58
Bizon:
źle Ci wyszło. Coś skaszaniłeś w przekształceniach
10 lut 00:06
qu: a2 = 1200− 4h2
i podstawiam to pod
v=1/3 a2 *h
10 lut 00:07
Eta:
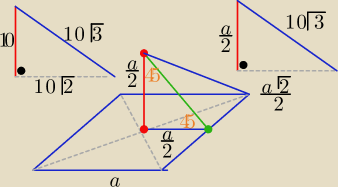
Bez pochodnych
Największa objętość będzie wtedy, gdy ściany boczny będą nachylone
pod kątem
45o do płaszczyzny podstawy
10 lut 00:10
qu: Musze to wyliczyć z równania i podstawić do −b/2a h−max
10 lut 00:14
Bizon:
| | a√2 | |
( |
| )2+h2=300 ⇒ a2+2h2=600 ⇒ a2=600−2h2 |
| | 2 | |
| | 1 | | 2h3 | |
V= |
| (600−2h2)h=− |
| +200h |
| | 3 | | 3 | |
10 lut 00:17
Eta:
V
'(h)=−2h
2+200 ⇒ V
'(h)=0 ⇒ h
2=100 ⇒ h=10
czyli tak jak na załączonym rysunku
10 lut 00:20
qu: poprosze prościej
skąd na tym rysunku po prawo wiadomo ze jest a √2 /2 ?
10 lut 00:57
Eta:
To długość połowy przekątnej kwadratu o boku "a" ( nie osłabiaj mnie na noc
10 lut 00:59
qu: Sory, musze to na jutro zrobić
Co dalej zrobić z wynikiem Bizona? Bo podobnie mi wyszło.
10 lut 01:16
Eta:
Policzyć pochodną ( [czyt. mój wpis 00:20
10 lut 01:17
qu: nie umiem pochodnych
To musi się dać zrobić bez pochodnych
Chciałem to podzielić ale nie ma wyrazu wolnego do znalezienia dzielnika
10 lut 01:22
Eta:
Zobacz co napisałam ( bez pochodnych) wpis 00:10 z rysunkiem
10 lut 01:25
qu: Czyli muszę wiedzieć o tych 45 stopniach ? niemożliwe
Wiesz co, dzięki za pomoc i tak już chyba dziś tego nie zrozumiem :
10 lut 01:34
Godzio:
Ja zaraz pokombinuje (ale nic nie obiecuje
)
10 lut 01:43
Human: Godzio, pomożesz mi z czymś innym?
10 lut 01:43
qu: ok, czekam
10 lut 01:45
Godzio:
Niestety, moje trudy na nic, jedynie do czego doszedłem to to, że h ∊ <6,10√3>. Może jeszcze
chwilę pomyśle, ale wątpię, żebym coś sensownego wymyślił.
10 lut 02:47
Godzio: O co chodzi Human ?
10 lut 02:47
Godzio:
Dobra wymyśliłem, trzeba to tylko trochę dopracować formalnie.
Z warunków dla trójkąta mamy:
h ≤ 10
√3 i h +
√600 − 2h2 > 10
√3 ⇔ h
2 + 2h
√600 − 2h2 + 600 − 2h
2 > 300
2h
√600 − h2 > h
2 − 300 /
2
4h
2(600 − h
2) > h
4 − 600h
2 + 90000
2400h
2 − 4h
4 > h
4 − 600h
2 + 90000
5h
4 − 3000h
2 + 90000 < 0
h
4 − 600h
2 + 18 000 < 0 ⇒ h ∊ <6,23>
h ∊ <6,10
√3>
Szukamy więc maksimum funkcji V(h) w tym przedziale
| | 2 | | 2 | |
V(h) = − |
| h3 + 200h = − |
| (h3 − 300h) |
| | 3 | | 3 | |
Rozważmy funkcję v(h) = h
3 − 300h
Chcemy znaleźć h, dla którego v(h) osiąga minimum. Weźmy sobie funkcję
G(h) = V(h) + a ≥ 0 dla h ≥ 0 (tak by minimum stało się miejscem zerowym)
| | 300 | | 100 | |
podstawmy h = x + |
| = x + |
| |
| | 3x | | x | |
| | 1 000 000 | |
Wtedy v(x) = x3 + |
| + a i podstawmy x3 = t |
| | x3 | |
| | 1 000 000 | |
v(t) = t + |
| + a |
| | t | |
h
3 − 300h + a ≥ 0 ⇒ t * (t
2 + at + 1 000 000) ≥ 0
Δ ≤ 0 ⇒ a
2 ≤ 4 000 000 ⇒ a ≤ 2 000
Weźmy a = 2000
G(h) = h
3 − 300h + 2000
Tutaj już można pobawić się w szukanie pierwiastków,
h
1 = 10
h
2 = −20
h = 10 jest szukanym argumentem
10 lut 03:08
qu: Dzięki, prostszym rozwiązaniem chyba będzie nauczenie się pochodnej
10 lut 22:07