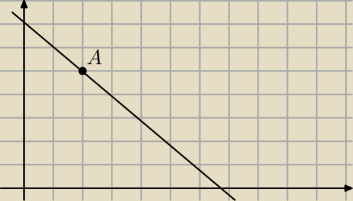
 Przez punkt A = (2,5) poprowadź taką prostą k o współczynniku kierunkowym
ujemnym, aby pole trójkąta ograniczonego osiami układu współrzędnych i
prostą k było najmniejsze. Podaj wzór tej prostej i oblicz pole tego trójkąta.
Ktoś jest chętny mi pomóc?
Przez punkt A = (2,5) poprowadź taką prostą k o współczynniku kierunkowym
ujemnym, aby pole trójkąta ograniczonego osiami układu współrzędnych i
prostą k było najmniejsze. Podaj wzór tej prostej i oblicz pole tego trójkąta.
Ktoś jest chętny mi pomóc? 
| 5−b | ||
wzór ogólny prostej: y=ax+b ... skoro przechodzi przez (2,5) to −> | = a | |
| 2 |
| 5−b | ||
więc masz wzór: y= | x+b | |
| 2 |
| 2b | ||
miejsce zerowe: x = | ||
| b−5 |
| b2 | ||||||||||||
pole trójkąta: | = | ||||||||||||
| 2 | b−5 |
 chociaż nie ma takiej konieczności
chociaż nie ma takiej konieczności

| b2 | b2−25 | 25 | 25 | ||||
= | + | = (b+5) + | |||||
| b−5 | b−5 | b−5 | b−5 |

