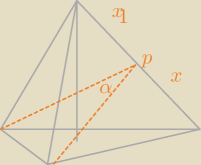
n Radek: jeśli mam ostrosłup praw. trójkątny i kat dwuścienny to to czy odległość x₁p x₂p jest zawsze równa ?

Mila: Nie.

Radek: Dziękuję, to już Pani rozwiała moje wątpliwości

Mila: Coś zapomniałeś o równaniach trygonometrycznych. Miało być jedno każdego dnia.

Radek: Ostatnio nie było mnie dwa dni, bo byłem chory i uzupełniałem barki które mam. Od jutra już będą tę równania. Teraz przerabiam wielomiany i z tym mam większy kłopot.

Mila: Powodzenia.

Radek: Za pół godzinki wstawię i proszę już o zaglądanie do mojego tematu jeżeli znajdzie Pani czas

Radek: Reszta z dzielenia wielomianu W (x) przez wielomian P (x) = x³ + 2²x − x − 2 jest równa x² + x + 1 . Wyznacz resztę z dzielenia wielomianu W (x ) przez wielomian V(x ) = x² − 1 . Proszę o wytłumaczenie bo mam problem z tymi zadaniami i chciałbym zrozumieć.

Mila: W(x)=(x³ + 2x ²− x − 2 )*Q(x)+(x²+x+1) V(x) =x²−1=(x−1)*(x+1) x=1, x=−1 pierwiastki V(x) Sprawdzimy czy P(x) jest podzielne przez (x²−1) P(1)=1+1−1−2=0 P(−1)=−1+2+1−2=0 tak jest podzielne ⇔w(1)=0+1+1+1=3 W(−1)=0+1−1+1=1 Reszta z dzielenia w(x) przez (x²−1) ma postać : r(x)=ax+b Teraz układ r(1)=3 i r(−1)=1 Dokończ.

Radek: Nie bardzo rozumiem czemu Pani tak zrobiła. Ale analizuję

Mila: Którego fragmentu nie rozumiesz?

Radek: Czemu Pani zapisuję tak ten wielomian W(x) ?

Mila: Jeżeli dzielisz wielomian przez P(x):

W(x)		R(x)
	=Q(x)+		⇔
P(x)		P(X)

W(x)		x2+x+1
	=Q(x)+		/*(x3 + 2x2− x − 2 )⇔
(x3 + 2x2− x − 2 )		(x3 + 2x2− x − 2 )

W(x)=(x³ + 2x²− x − 2 )*Q(x)+(x²+x+1)

Radek: Dziękuję teraz już chyba rozumiem.

Mila: To dokończ i napisz wynik.

Radek: a=1 b=2 R(x)=x+2

Mila: Dobrze.

Radek: Jeszcze jutro wstawię kilka zadań bo mam sprawdzian powtórkowy i chcę dobrze napisać. Dobranoc.

Mila: Dobranoc

Radek: Czyli te zadania z podzielnością wszystkie robi się tak samo. ?

Mila: Podobnie.

Radek: To jeśli Pani ma czas to wrzucę kilka zadań.

Radek: Reszta z dzielenia wielomianu W (x) przez wielomian P(x)=x⁴+x³−3x² − 4x − 4 jest wielomianem R(x) = x³−5x+1. Wyznacz resztę z dzielenia tego wielomianu przez wielomian F (x) = x² − 4

Mila: 1) Oblicz miejsca zerowe F(x) 2) sprawdź czy p(x) ma takie miejsca zerowe jak F(x) 3) jaka postac będzie miała reszta z dzielenia w(x) przez f(x)?

Radek: F(x)=(x−2)(x+2) x=2 lub x=−2 P(x)=(x−2)(x+2)(x²+x+1)

Mila: Dobrze . W takim razie : W(X)=(x−2)(x+2)(x²+x+1)*Q(x)+x³−5x+1 Teraz oblicz w(−2) i w(2) r(x)=ax+b wielomian st. pierwszego. dalej sam.

Radek: 3a+b=0 −a+b=0 o takie coś chodzi ?

Radek: ?

Mila: dlaczego =0? w(−2)=0*Q(x)+(−2)³−5*(−2)+1=−8+10+1=3=r(−2) W(2)=0*Q(x)+2³−5*2+1=8−10+1=−1=r(2) −2a+b=3 2a+b=−1 2b=2, b=1, a=−1 r(x)=−x+1

Radek: Bo w(2) było pierwiastkiem tak ?

Mila: Tak wyzerowała się część : ((x−2)(x+2)(x2+x+1)*Q(x) a dla reszty obliczyłeś wartość.

Radek: (−2)³−5(−2)+1=3 (2)³−5*2+1=−1

Radek: Już wiem, dziękuję ślicznie

Mila:

Radek: Jeszcze tylko proszę o pomoc w tych równaniach kwadratowych jak Pani znajdzie chwilkę czasu dla mnie.

Mila: Jeszcze jestem.

Radek: Nie pamiętam treści ale chodzi o takie zadania (równania) trzeba wyznaczyć parametr dla którego pierwiastki należą do przedziału o takie zadania mi chodzi

Mila: Znajdę jutro, bo teraz nie wiem, gdzie ma zbiór?

Radek: Już znalazłem i zaraz podaję treść. Dla jakich wartości parametru m pierwiastki równania x²−2mx−m−2=0 są zawarte między liczbami −2 i 4 ? Δ≥0

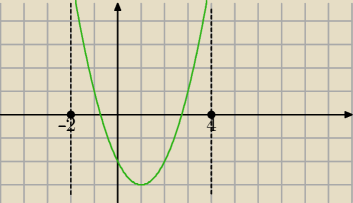
Mila: 1)Δ≥0 2)−2<x_w<4 3) f(−2)>0 i f(4)>0

Radek: Dziękuję, w życiu bym na to nie wpadł.. Jestem bardzo wdzięczy za Pani pomoc. !

Radek: Czyli będę miał 3 warunki 1 2 3 część wspólna i potem cześć wspólna 1,2,3 ?

Mila: Rozwiąż.

Radek: Δ≥0 (2m)²−4(−m−2)≥0 4m²+8m+8≥0 Δ_m<0⇔m∊R f(−2)>0 4+4m−m−2>0 3m>−2

	2
m>−
	3

f(4)>0 16−8m−m−2>0 −9m>−14

	14
m<
	9

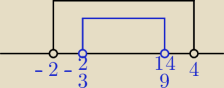
	2		14
czyli z 3 warunku m∊(−		,		)
	3		9

m>−2 i m<4 m∊(−2,4) ?

Mila: Jaką dajesz odpowiedź?

Radek:

	2		14
m∊(−		,		)
	3		9

Mila: Tak. Dobranoc

Radek: Dobranoc. I jeszcze raz dziękuję