geo qudis: Różnica długości boków równoległoboku jest równa 11 cm.Pole równoległoboku wynosi 168cm2 a cosinus kąta ostrego jest równy 0,6.Wyznacz krótszą wysokość oraz krótszą przekątną. Prosze o pomoc

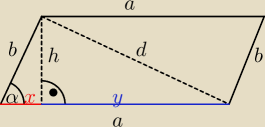
agulka: Dane: a−b=11 P=168 cosα=0,6⇒cos²α=0,36 Pole równoległoboku: P=a*b*sinα. sin²α+cos²α=1 sin²α=1−0,36 sinα=0,8 P=a*b*sinα 168=a*b*0,8 a*b=210 Otrzymuję układ równań:

⎧	a*b=210
⎩	a−b=11

Stąd otrzymuję: a=21 i b=10 P=a*h 168=21*h h=8 x+y=a⇒x+y=21

	x
cosα=
	b

b*cosα=x x=6 y=15 d²=h²+y² d²=64+225 d²=289 d=17

Eta:

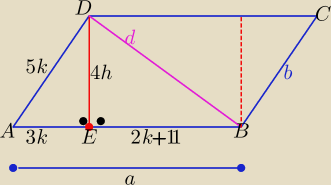
	3
cosα=		, b=5k i a−b=11⇒ a= 5k+11 , |EB|=2k+11 , k>0
	5

	4
sinα=
	5

	4
P=a*b*sinα ⇒ 5k(5k+11)*		=168 ⇒ k(5k+11)=42 ⇒ k=2
	5

to: b=10 cm, a= 21 cm , h=8 cm , |EB|=15 cm , d= √8²+15²= 17 cm

wero: dzieki

Eta: