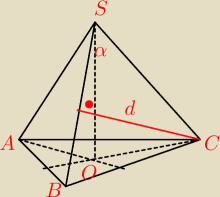
Bryła bezendu: W ostrosłupie prawidłowym trójkątnym kąt płaski przy wierzchołku ostrosłupa ma miarę α , zaś odległość wierzchołka podstawy od krawędzi bocznej, do której nie należy, jest równa d . Oblicz objętość

	d
|SC|=
	sinα

	√3a
|OC|=
	6

	d		√3a
H2=(		)2−(		)2
	sinα		6

	36d2−3asin2α
H2=
	36sin2α

H=U{√36d²−3a²sin²α{6sinα}

	a2√108d2−9asin2α
V=
	72sinα

W odpowiedzi mam wgl inaczej ?

Bizon:

	2		a√3
|OC| to		*
	3		2

bezendu: To i tak nadal wychodzi zła odpowiedź.

Mila: V ma byc zależne od α i d. Nie widzę ,żeby w treści podano a. I to OC popraw.

bezendu:

	a2√3
|OC|=
	3

bezendu: To ile będzie kąt ∡SBC ?

Mila:

	α
∡SBC =(180−α):2=90−
	2

bezendu: Kąty połówkowe.. pomyślę nad tym zadaniem. Dziękuję.

Mila: Nie przejmuj się tym kątem, jest dany. W ΔCDB:

	α		d		α		d
sin(90−		=		⇔cos		=
	2		a		2		a

	d
a=
	α   cos   2

Licz dalej

bezendu:

	α   d3√3cos2 −sin2α   2
Racja wzory redukcyjne V=
	α   12sinαcos   2

w liczniku oprócz d³ wszystko jest pod pierwiastkiem.

Mila:

	α
w mianowniku 12 sinα*cos3		?
	2

bezendu: Tak, zjadałem 3 przepraszam.

Mila: Nie szkodzi. Mamy złoty medal.!

Ajtek: Mila

bezendu: Tak, wiem oglądałem w między czasie

Marcin: Yeah! Jeszcze 2 medale dla Kamila!

bezendu: I może dla Justyny ?

Marcin: Pewnie, chociaż na pewno ciężko będzie jej ze złamaną stopą

Mila: Dobranoc