zadanko
miszczu: |x|+|y|=2
y−x=m
przedstaw liczbę rozwiązań w zależności od parametru m.
prosszę pomocy
9 lut 14:56
miszczu: pomoże ktoś?
9 lut 15:17
MQ:
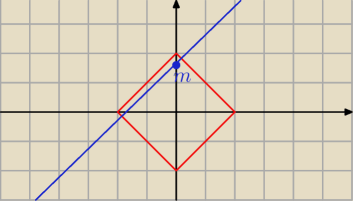
9 lut 15:52
Mila:
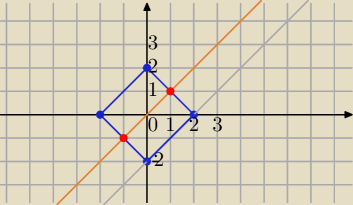
Metoda graficzna :
|x|+|y|=2
y=x+m
y=x
1) dla m<−2 brak rozwiązań
2) Dla m=−2, y=x−2 nieskończenie wiele rozwiązań: (x,x−2), x∊<0,2>
3)
m∊(−2,2) dwa rozwiazania
4) m=2 nieskończenie wiele rozwiązań (x,x+2), x∊<−2,0>
5) m>2 brak rozwiązań.
9 lut 15:55
miszczu: dlaczego y=x?
9 lut 19:16
Mila:
y−x=m
⇔y=x+m
y=x prosta przechodząca przez (0,0)
y=x→T[0,m] →y=x+m ( przesunięcie równoległe prostej y=m)
9 lut 19:36
miszczu : Czyli jeżeli mialbym takie podobne zadanie to moge sobie m obrać jako punkt 0,0?
9 lut 20:57
Mila:
To zależy od zadania. Tutaj przesuwasz równolegle prostą y=x
9 lut 21:32