Cosinus kąta między ścianami bocznymi i współrzędne pkt d Seb: Mam problem z 2 zadaniami: 1. W ostrosłupie prawidłowym czworokątnym krawędzie boczne są 2 razy dłuższe od krawędzi podstawy. Ile wynosi cosinus kąta zawartego między ścianami bocznymi tego ostrosłupa ? 2. Dany jest trójkąt ABC gdzie A (−1; 2) B (0;4) C (4;4) Wys opuszczona z wierzchołka A na bok BC przecina go w punkcie D. Znajdź współrzędne punktu D.

dero2005:

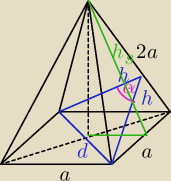
	√15
hs = √(2a)2 − (a2)2 =		a
	2

a*h_s = n*2a

	a*hs		√15
n =		=		a
	2a		4

d = a√2 d² = 2h² − 2h²cosα cosα =

Seb: Ok dzięki. Może ktoś jeszcze pomóc z 2?

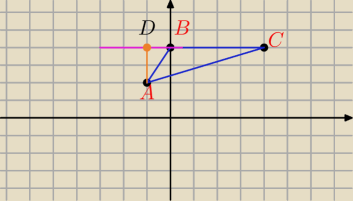
5-latek: Z rysunku wszystko widac

Seb: Oj pomyłka w punkcie b miało być −4 na osi y nie 4.

dero2005:

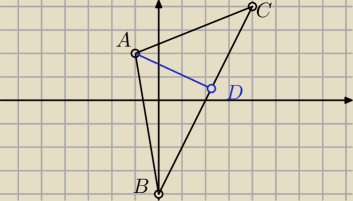
	yC−yB		4+4
aBC =		=		= 2
	xC−xB		4−0

y_BC = a_BC(x−x_B)+y_B = 2x − 4

	−1
aAD =		= −12
	aBC

	1		3
yAD = aAD(x − xA)+yA = −		x +
	2		2

y_AD = y_BC

	1		3
2x − 4 = −		x +
	2		2

	11
x =
	5

	2
y =
	5

D(¹¹₅, ²₅)