najmniejsza i najwieksza wartosc funkcji CzasNastal:

	pi
f(x)=2sinx−x przedział [0,		] Liczę f(x)' wtedy wyjdzie f(x)'=2cosx−1 i co teraz?
	2

Rysuję wykres cosinusa, opuszczam go o 1 względem osi Y (nie wiem co z tą 2 zrobić przed cos.). I wtedy patrzę na przedział i największa/najmniejszą wartość + sprawdzam jakie są wartości na krańcach(bo mogą być większe/mniejsze od tych w przedziale). Dobrze kombinuję?

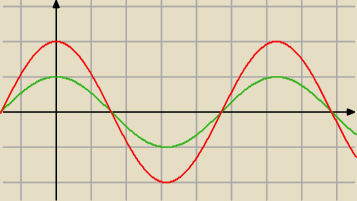
Ajtek: Masz narysować 2*cosx, czyli rozciągnąć wykres w pionie 2 razy. Zielony − cosx Czerwony − 2*cosx

J: Funkcja może posiadać ekstremum w punkcie zerowania się pierwszej pochodnej.Aby posiadała,druga pochodna w tym punkcie musi być różna od zera i jeśli jest dodatnia to funkcja ma minimum,jeśli ujemna to maximum.

CzasNastal: a to −1 coś zmienia nasz wykres?

Ajtek: Tak, opuszczasz go o jeden .

CzasNastal: okej i jak teraz wyliczyć tą najmniejszą i największą wartość funkcji? Największa będzie w y=1

	pi
dla x=0, a najmniejsza wartość funkcji w y=0 dla x=		, tak?
	2

CzasNastal: Dobrze mówię? Czy to co wyżej podałem jest błędną odpowiedzią?

J: Ty masz obliczyć ekstremum funkcji f(x)=2sinx − x , a nie jej pochodnej.

CzasNastal: Czyli jak mam to zrobić? Jak narysuję wykres 2sinx−x?

J: Przeczytaj post 13:12. Tutaj nie misisz rysować wykresu pochodnej, tylko na podstawie jej analizy ustalić ekstremum funkcji f(x)

CzasNastal: No dobra, także z tego postu co napisałeś o 13:12 mogę stwierdzić czy ta funkcja ma minimum czy maximum. Ale na co mam patrzeć(na który wykres) żeby podać najmniejszą i największą wartość funkcji? Bo o to mnie pytają w zadaniu

J:

	π
Masz sprawdzić,czy funkcja f(x) = 2sinx − x posiada ekstremum w przedziale <0,		>.
	2

Liczysz pierwszą pochodną i sprawdzasz czy zeruje się w tym przedziale.Jeżeli tak,to w punkcie zerowania może ( ale nie musi) posiadać ekstremum.Decyduje o tym wartość drugiej pochodnej w tym punkcie. Jeśli jest rózna od zera to w tym punkcie jest ekstremum.

CzasNastal:

	pi
f(x)'=2cosx−1 , gdy przyrównam do zera (cosx=		)
	3

f(x)''=−2sinx i tu sinx=0, tak? I co teraz?

J:

	1		π
2cosx−1 = 0 ⇔ cosx =		⇔ x =
	2		3

	π		π		√3
Liczymy wartość drugiej pochodnej : f"(		) = −2sin(		) = −2		= −√3
	3		3		2

	π
Poniważ druga pochodna jest ujemna, więc funkcja f(x) posiada maximum w punkcie x=
	3

CzasNastal: a minimum nie ma? Chyba musi być gdzieś to minimum

J: Funkcja f(x) = 2sinx − x ma nieskończenie wiele ekstremów, ale w tym konkretnym przedziale tylko jedno i jest to maximum ( tzw. extremum lokalne)

CzasNastal: Okej już rozumiem, dziękuję bardzo