trójkąty
komik: Dany jest trójkąt prostokątny ABC i trójkąt równoboczny DEF o boku równym przeciwprostokątnej
trójkąta ABC. Pole DEF jest dwa razy większe od pola trójkąta ABC. Wykaż, że katy ostre
trójkąta prostokątnego mają miary 30 i 60.
doszedłem do czegoś takiego :
(a2+b2)√3=4ab
8 lut 21:04
komik:
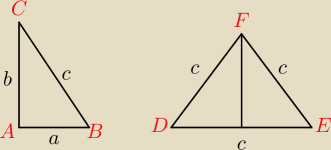
8 lut 21:13
komik: pomoże ktoś ?
8 lut 21:22
Bizon:
równanie, które wyprowadziłeś podziel stronami przez a
2
| | b | | b | | √3 | | b | |
policzysz |
| =√3 lub |
| = |
| a wiesz, że: |
| =tgβ |
| | a | | a | | 3 | | a | |
8 lut 21:26
komik: Dzięki wielkie

8 lut 21:28
pigor: ..., no to dalej niech α+β=90
o miary kątów ostrych ΔABC, to
(a2+b2)√3=4ab /:ab ⇔ (
ab+
ba)
√3=4 ⇔ (tgα+ctgα)
√3=4 /*tgα ⇔
⇔
√3tg
2α+
√3= 4tgα ⇔
√3tg2α−4tgα+√3= 0 −równanie kwadratowe
zmiennej tgα i Δ=16−12= 4,
√Δ=2 i tgα=
12√3(4−2) v tgα=
12√3(4+2) ⇒
⇒ tgα=
13√3 v tgα=
√3 ⇒
α=30o v α=60o c.n.w. ...

8 lut 21:29


