ciagi ona: zbadaj monotonicznosc ciagow a_n=2n+1 b_n=²ⁿ_n+3 c_n=n²−2n+2 d_n=ⁿ⁻⁵_n+1

sushi_ gg6397228: przepis znasz ?

ona: nie

bezendu: a_n+1 a_n+1−a_n

ona: prosze mi to rozpisac bo nie rozumiem za bardzo

5-latek: bezendu tutaj niestety trzeba dac gotowca . ta Pani jest 28 lat po szkole

ona: no i co na zlosliwosciach sie skonczylo ?

Marcin: 5−latek , ale daj już Pani spokój

sushi_ gg6397228: podany jest przepis: a_n= ... a_n+1=.... podstawiamy i mamy .....

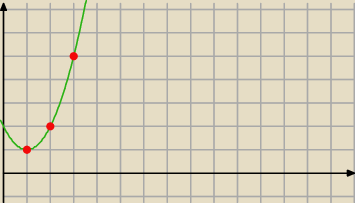
Bizon: a można np tak kolejne wyrazy ciągu c_n=n²−2n+2 "układają się na wykresie paraboli ....zatem ...

ona:

5-latek: Marcin ale ja Pani wcale nie dokuczam . Nie mam nawet takiego zamiaru . W porzednim poscie sama przeciez napisala ze jest 28 lat po szkole i nic nie rozumie . jesli tak jest to jest o 10 lat mlodsza ode mnie

	2n
Zeby nie bylo ze jestem zlosliwy to np bn=
	n+3

jesli b_n+1−b_n>0 to ciag jest rosnacy jesli b_n+1−b_n<0 to ciag jest malejacy jesli b_n+1−b_n=0 to ciag jest staly Liczymy wyraz b{_n+1} w miejsce n a wyrazie b_N wstawiamy n+1 i mamy

	2(n+1)		2n+2
bn+1=		=
	(n+1)+3		n+4

	2n+2		2n
teraz b{n+1}−bn=		−		= do wspolnego mianownika i mamy=
	n+4		n+3

	(2n+2)(n+3)−2n(n+4)		2n2+8n+6−2n2−8n		6
		=		=
	(n+4)(n+3)		(n+4)(n+3)		(n+4)(n+3)

Teraz jest najtrudniejszy moment w takim zadaniu bo trzeba wyciagac wniski bo od razu nie widac jaki to ciag Licznik =6>0 mianownik jest tez >0 bo n nalezy do N₊ wiec jest dodatni . Ztego wnnoisek ze jesli licznik jest dodatni i mianownik jest dodatni to caly ulamek jet dodatni czyli >o wiec ten ciag jest rosnacy . Tyle

Bizon: a można tak: a_n+1−a_n=2(n+1)+1−2n−1=2 jaki? a można tak:

bn+1		2(n+1)		n+3		(n+1)(n+3)
	=		*		=		=
bn		n+1+3		2n		n(n+4)

	n2+4n+3		3
=		=1+		... i wnioski −
	n2+4n		n2+4n

ona: dziekuje slicznie

5-latek: NO to niech teraz policzy wyraz c_n+1