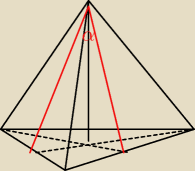
bryły bezendu: kąt między ścianami bocznymi ostrosłupa prawidłowego trójkątnego ? Czyli to jest kąt pomiędzy wysokościami ścian bocznych ?

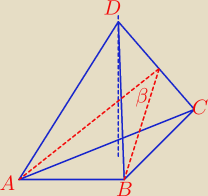
Piotr 10: tak też dobrze jest rysować, też dobrze widaćβ prowadzisz wysokości ściany ACD i ściany BDC, czyli ok

bezendu: Ale moje też ok ?

Godzio: Właśnie dałeś sobie zadanie. Sprawdź czy α = β

bezendu: Trochę to potrwa Ale policzę.

Piotr 10: Chyba tak, bo to jest kąt utworzony przez wysokości ścian bocznych. Ja narysowałem tak, bo dla mnie lepiej jest robić zadania z tym kątem dwuściennym( lepiej widać)

Piotr 10: Oj chyba jednak źle napisałem sorki

Godzio:

Godzio: No i jak tam, rozwiązanie nie jest aż takie długie

bezendu: Mój kat wychodzi poprawnie

Godzio:

	1
h2 = b2 −		a2
	4

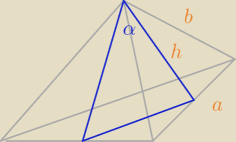
Z twierdzenia cosinusów:

	1		8b2 − 3a2
(		a)2 = h2 + h2 − 2h2cosα ⇒ cosα =
	2		8b2 − 2a2

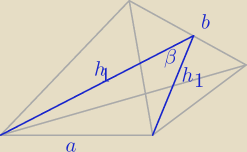
Godzio: Z przyrównania pól:

bh1		ah		1   a2 * (b2 − a2)   4
	=		⇒ h12 =
2		2		b2

Z twierdzenia cosinusów:

	2b2 − a2
a2 = h12 + h12 − 2h12cosβ ⇒ cosβ =
	4b2 − a2

Widać, że w ogólnym wypadku tak nie jest. Kąty będą równe tylko wtedy gdy zajdzie warunek: a = 2b

Godzio: Kąty nie są równe, a szukanym kątem (między ścianami) jest kąt β.

Godzio: Napisałem bzdurę na koniec Równości nigdy nie będzie

Mila: Bezendu, nie załamuj mnie, przecież to juz wyjaśnialiśmy.

bezendu: No tak ale wolę się upewnić.

bezendu: Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod kątem 6 0^∘ . Odległość spodka wysokości ostrosłupa od krawędzi bocznej jest równa 4. Oblicz objętość tego ostrosłupa.

	128√3
V=		j3 ?
	3

Piotr 10: Tak samo mi wyszło

bezendu: Dzięki.

bezendu: Podstawą ostrosłupa ABCS jest trójkąt równoramienny ABC w którym |BC|=|AC|=40 i |AB|=40. Każda krawędź boczna ma tę samą długość równą 30. Oblicz objętość tego ostrosłupa P_p=768 H=5√11 V=1280√11j³ ?

bezendu: |AB|=48 przepraszam za pomyłkę.

Marcin: A ja kurde liczę dla trójkąta równobocznego nono, bezendu cześć

Piotr 10: P_p ok H ok V ok tak samo mam

bezendu: Witam.

Marcin: Mógłbym się dowiedzieć z czego liczycie tą wysokość ostrosłupa?

bezendu: Z tw. Pitagorasa.

Mila: To, gdzie leży spodek wysokości tego ostrosłupa?

Marcin: hehe dzięki śmieszku, ale na to wpadłem sam

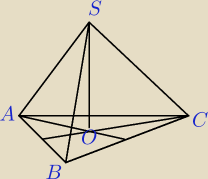
bezendu: Może rysunek nie najlepszy ale |OC|= promień okręgu opisanego na trójkącie ABC

Mila: Tak jest!.

bezendu: A jeśli w podstawie miałbym romb to promień wpisanego w romb. ?

Mila: Rombem to różnie bywa.

bezendu: A można jaśniej bo mam romb w podstawie ostrosłupa i również muszę wyliczyć V to zrobiłem okrąg wpisany i wyszło..

Mila: Podaj treść.

bezendu: Ja zrobiłem to zadanie. Romb o boku długości 12√3 i kącie ostrym 30⁰ jest podstawą ostrosłupa. Każda ściana boczna ostrosłupa jest nachylona do płaszczyzny podstawy pod katem 60⁰. Oblicz V tego ostrosłupa V=648j³

Mila: Jeżeli każda ściana nachylona pod tym samym kątem, to spodek wysokości ostrosłupa leży w środku okręgu wpisanego w podstawę.

bezendu: A jak może być jeszcze inna sytuacja z rombem w podstawie jeśli będę miał ostrosłup ? Chyba tylko taka. ?

Mila: Na ogół, tak, kłopot sprawia uczniom obliczenie powierzchni bocznej.

bezendu: Dziękuję za odpowiedź Idę robić kolejne zadania z którymi mam problem.

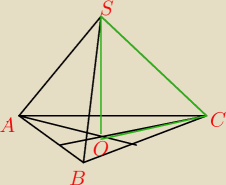
bezendu: Z tym mam kłopot: Oblicz cosinus kąta między ścianą boczną i płaszczyzną podstawy ostrosłupa prawidłowego trójkątnego, jeżeli wiadomo, że promień okręgu opisanego na podstawie, wysokość ostrosłupa i krawędź boczna tworzą trójkąt równoramienny Czyli |OC|=|SO| ?

Godzio: Tak

bezendu:

	√5
Wyszło cosα=		?
	5

Mila: Zgadza się.

bezendu: Dziękuję.

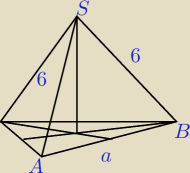
bezendu: W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 6, a pole ściany bocznej jest równe 9√3 . Oblicz objętość tego ostrosłupa.

1
	*a*h=9√3
2

	a
h2=62−		2
	2

	a2
h2=36−
	4

	144−a2
h2=
	4

h=U{√144−a²{2}

1
	ah=9√3
2

ah=18√3

	√144−a2
a*		=18√3
	2

a√144−a²=36√3 / ² a²(144−a²)=3888 a⁴−144a²+3888=0 t=a² t>0 t²−144t+3888=0 √Δ=72 t₁=36 t₂=108 a=6 lub 6√3 Wyjdą dwa rozwiązania ?

bezendu: jeśli wezmę a=6 to V=18√2 a dla a=6√3 wychodzi sprzeczność bo H=0 ?

bezendu: ?

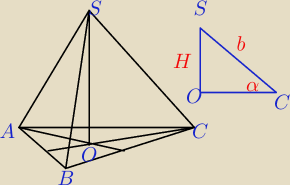
bezendu: Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość b i tworzy z płaszczyzną podstawy kąt o mierze α . Jaką objętość ma ten ostrosłup?

	H
b=
	sinα

H=bsinα |OC|²=b²−b²sin²α |OC|²=b²(1−sin²α) |OC|=bp{1−sin²α) |OC|=bcosα

	2h
|OC|=
	3

2h
	=bcosα
3

2h=3bcosα

	3bosα
h=
	2

a√3		3bcosα
	=
2		2

a=√3bcosα

	(√3bcosα)2√3
Pp=
	4

	3√3cos2α
Pp=
	4

	1		3√3bcosα
V=		*		*bsinα
	3		4

	√3b2cos2αsinα
V=
	4

bezendu: Ktoś chętny na sprawdzenie tych dwóch zadanek ?

bezendu: Poprawka:

	3√3b2cos2α
Pp=
	4

	√3b3cos2αsinα
V=
	4

Godzio: Jest ok.

bezendu: ale chodzi o zadanie 23:14 dobre założenie odnośnie t ?

bezendu: ?

bezendu: W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 3√6 , a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne α=120⁰

bezendu: ?

Piotr 10:

	1
tak samo mi wyszło cosα=−
	2

a więc 120⁰

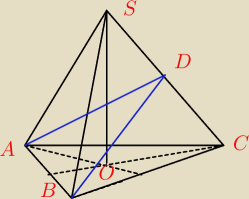
bezendu: Dany jest ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość a i krawędź boczna jest od niej dwa razy dłuższa.. Narysuj przekrój ostrosłupa płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej krawędzi bocznej. Czy to trójkąt ABD ?

Piotr 10: tak

bezendu: a 23:14 ?

bezendu: I jeszcze wracając do zadania 14:19 jak obliczyć pole tego przekroju ? Skoro AD anie BD nie są wysokościami ścian bocznych ?

bezendu: ?

bezendu: Podpowie ktoś ?

bezendu: ?

Mila: BD jest środkową , SD=DC=a

bezendu: Dziękuję

bezendu:

	a2√5
Pprzekroju=
	4

bezendu: ?

Mila: Tak.

bezendu: Dziękuję jeszcze 3 zadanka wstawię za chwilę.

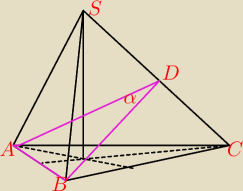
bezendu: W ostrosłupie trójkątny krawędź boczna jest 3 razy dłuższa od krawędzi podstawy. Oblicz cosinusa kąta zawartego pomiędzy ścianami bocznymi tego ostrosłupa.

	√35a2
Pole ściany bocznej BSC=
	4

	√35a2
|BD|=|AD|=
	6

	√35a2		√35a2		√35a		√35a
a2=(		)2+(		)2−2*		*		*cosα
	6		6		6		6

	35a2		35a2		35a2
a2=		+		−
	36		36		18

	35a2		35a2cosα
a2=		−
	18		18

	35a2		35a2cosα
a2−		=−
	18		18

18a2−35a2		35a2cosα
	=−		/18
18		18

−17=−35cosα cosα=U{17}{35{

	39
w odpowiedzi cosα=
	70

Gdzie jest błąd ?

bezendu:

	17
cosα=
	35

Mila: Dobrze masz.

bezendu: Dziękuję, czyli jednak błąd w odpowiedziach..