Funkcje trygonometryczne maramasike: 1.Katy α i β są kątami ostrymi takimi, że: sinα=0,6 i tgβ=2. Oblicz wartość wyrażenia 2sinβ*tgα+cosα*cthβ−3. 2. W trapezie równoramiennym cos kąta ostrego wynosi 2/3, a wys. jest równa 8 cm. Oblicz obw. trapezu, wiedząc, że krótsza podstawa trapezu ma dł. 8 cm. 3. Ramię trójkąta równoramiennego ma dł. 10 cm, a kąt przy podstawie ma miarę 30 stopni. Oblicz obw. i pole tego trójkąta oraz promień okręgu wpisanego w ten trójkąt i promień okręgu opisanego na nim. 4. Kąty ostre α i β trójkąta prostokątnego spełniają warunek sinα*tgβ=1/3. Oblicz: a) sumę sinusów kątów ostrych tego trójkąta b) sumę cosinusów kątów ostrych tego trójkąta.

Domel: 1. sinα=0,6 => cosα=√1−sin²α = √1−0,6² = √0,64 cosα=0,8 tgα = sinα/cosα = 0,6/0,8 tgα=0,75 cgtβ=1/tgβ ctgβ=0,5 sinβ = cosβ*tgβ = 2cosβ = 2*√1−sin²β sin²β=4*(1−sin²β) = 4 − 4sin²β 5sin²β=4 => sin²β = 4/5 sinβ = 2√5/5 Więc równanie ma postać: 2sinβtgα+cosαctgβ−3=2*0,75*2√5/5 + 0,8*0,5 − 3 = 3√5/5 − 2,6

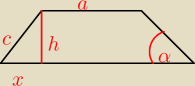
Domel: 2. cosα=x/c = 2/3 h=8 a=8 sinα=√1−cos²α = √1−(4/9) = √5/9 sinα = √5/3 tgα = sinα/cosα = √5//3 * 3/2 tgα = √5/2 tgα=x/h => x = h*tgα = 8*√5//2 x = 4√5 x/c=2/3 => c = 3x/2 = 3*4√5//2 c = 6√5 Więc obwód S wynosi S = 2a + 2c + 2x = 2*(a+c+x) = 2*(8+6√5+4√5) = 2*(8+10√5) S = 16 + 20√5

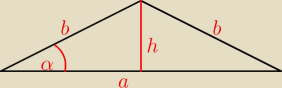
Domel: 3. b=10 cm α=30° h/b = sinα => h = bsinα = 10*0,5 h=5 0,5a/h = tgα => 0,5a = htgα => a = 2htgα = 2*5*√3/3 a=10*√3/3 Obwód: S = a + 2b = 10*√3/3 + 20 = 10(2+√3/3) Pole pow.: P = 0,5ah = 0,5*5*10*√3/3 = 25*√3/3 Promień okręgu opisanego na trójkącie R = b/2sinα = 10/(2*0,5) = 10 Promień okręgu wpisanego w trójkąt r=2P/(a+2b) = 2*(25*√3/3)/(20+10*√3/3) = (50*√3/3)/(20+10*√3/3) r=5*(√3−1)/11

Domel: 4. α=90°−β => sinα = sin(90°−β) sinα = cosβ sinα*tgβ = 1/3 => cosβ*tgβ = cosβ*sinβ/cosβ = 1/3 sinβ=1/3 cosβ = √1−sin²β = √1−(1/3)² = √8/9 cosβ = 2√2/3 sinα = cosβ sinα = 2√2/3 cosα = √1−sin²α = √1−(2√2/3)² = √1−(4*2/9) = √(9−8)/9 = √1/9 cosα = 1/3 Możemy podstawiać: a) sinα + sinβ = 2√2/3 + 1/3 = (1+2√2)/3 b) cosα + cosβ = 1/3 + 2√2/3 = (1+2√2)/3