:)
Mat: ile jest liczb naturalnych trzycyfrowych wzglednie pierwszych z liczba 70 ?
7 lut 22:54
Mat: szukamy liczb ktore nie dziela sie przez 2,5,7,10 i ich jedyny wspolny dzielnik z liczba 70 to
1, tak ? I jak tego szukać ?
7 lut 22:58
Mat: ?
7 lut 23:04
bezendu: Najpierw zobacz definicję liczby względnie pierwszej....
7 lut 23:05
Mila: |Ω|=900
W− liczba trzycyfrowa względnie pierwsza z liczbą 70
A2− liczba trzycyfrowa podzielna przez 2
A5− liczba trzycyfrowa podzielna przez 5
A7− liczba trzycyfrowa podzielna przez 7
i teraz sporo liczenia
P(A2UA5UA7)=
=P(A2)+P(A5)+P(A7)−P(A2∩A5)−P(A2∩A7)−P(A5∩A7)+P(A2∩A5∩A7)
P(W)=1−P(A2UA5UA7)
7 lut 23:08
Mat: no to dobrze mysle czy nie ?
7 lut 23:24
Mat: Mila moglabys powiedziec co dalej ? Nie bardzo rozumiem jak to liczyc
7 lut 23:26
Mila:
Rozumiesz co napisałam? wiesz jak masz liczyć?
7 lut 23:26
bezendu:
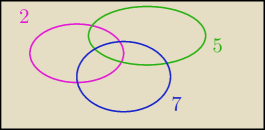
|A∪B∪C|=|A|+|B|+|C|−|A∩B|−|B∩C|−|A∩C|+|A∩B∩C|
|A|−podzielne przez 2
|B|−podzielne przez 7
|C|podzielne przez 5
A potem tak jak napisał
Mila
1−|A∪B∪C|
7 lut 23:31
MQ: Trochę mu w głowie mieszacie.
On ma policzyć liczbę względnie pierwszych, a nie prawdopodobieństwo otrzymania takiej
liczby, więc na pewno nie 1−P(A2UA5UA7)
7 lut 23:34
Mila:
1) liczby podzielne przez 2
900:2=450
albo z ciągu
a1=100
an=998, 998=100+(n−1)*2⇔998=100+2n−2⇔2n=900, n=450
2) liczby podzielne przez 5
a1=100
an=995
995=100+(n−1)*5
oblicz
3)liczby podzielne przez 7
a1=105
an=994 ,994=105+(n−1)*7 licz
4) liczby podzielne przez 2 i 5
a1=100,
an=990, 990=100+(n−1)*n
5)
Dalej będziesz wiedział?
Ja już idę spac, jutro spojrze.
7 lut 23:35
Mat: No to moglby ktos napisac czy jest jakis algorytm wyliczania tego czy jak ? no zadne
prawdopodobienstwo tylko ile ich jest
7 lut 23:36
Mat: to na jutro na egzamin ...
7 lut 23:37
Mila:
Rzeczywiście , ilość. 23:35 aktualne.
900− |A∪B∪C|
7 lut 23:38
bezendu:
to policz 5) liczby podzielne przez 2 i 7
6) liczby podzielne przez 5 i 7
7) liczby podzielne przez 2,5,7
7 lut 23:38
Mila: Mat umiesz to policzyć?
|A2UA5UA7|=
=|A2|+|A5|+P|A7|−|A2∩A5|−|A2∩A7|−|A5∩A7|+|A2∩A5∩A7|
7 lut 23:45
Mat: pewnie tak ale jak to widze to za duzo tego liczenia ... za duze prawdopodobienstwo ze pomyle
sie w obliczeniach

jak mowicie ze nie ma innego sposobu ....

7 lut 23:47
Mat: może dam prostrze zadanie?
Ile jest liczb w zb 1−280 wzglednie pierwszych z liczba 280 ?
7 lut 23:52
Mat: w naturalnych od 1 do 280
7 lut 23:53
Mat: tzn mialo byc ile nie jest
wyszlo mi ze jest 44 liczby wzglednie pierwsze z 280 w tym zb
jak myslicie ?
7 lut 23:56
Mat: ?
8 lut 00:35
Aga1.: 280=2*2*2*5*7
D280={1,2,4,5,7,8,10,20,28,40,56,280}
Teraz wypisz liczby, które nie są podzielne przez wymienione liczby ( nie wiem czy jest szybszy
sposób)
3,9,11,13,17,19,23,29,31,33,...
8 lut 09:01
Mat: No trochę by mi zeszło obliczenie ile ich jest ...
Odświeżam temat. Ktoś ma pomysł>?
I zadanie może łatwiejsze np.Ile jest liczb trzycyfrowych względnie pierwszych z 63 ?
63=3*3*7
Szukamy liczb trzycyfrowych podzielnych przez 3 i 7 ?
14 lut 12:53
Mat: podzielnych przez 7 jest 128 liczb
podzielnych przez 3 jest 300 liczb
podzielnych przez 3 i 7 jest 43 liczby
Odp: 900−128−300−43 ?
POWIE KTOŚ >?
14 lut 13:02
Mat: znaczy sie + 43
14 lut 13:03
hadron: Czy i jaki jest wzór na obliczenie ile kul o średniczy 1 cm mieści się w kuli o średnicy 3 cm?
14 lut 13:22
Mat: poszukaj gdzie indziej
14 lut 13:23
hadron: dzięki za podpowiedź − słyszałem, że 13 kul ale chciałbym to sprawdzić matematycznie
14 lut 13:34
Mila:
63=3*3*7, tu są 2 czynniki równe 3.
900− tyle jest liczb trzycyfrowych
A3 − liczby trzycyfrowe podzielne przez 3, wśród nich sa podzielne przez 9
|A3|=300
|A7|=128
A7∩A3− liczby podzielne przez 7 i 3⇔przez 21,wśród nich sa podzielne przez 63
|A7∩A3|=43
900−(300+128−43)=900−385=515
14 lut 18:24
Panko: Może trzeba skorzystać z funkcji Eulera ?
70=2*5*7
980=22* 5*72
Niech n ≤999, jeżeli (n,70)=1 ⇔(n, 980)=1 (?)
φ(980) −−−to te szukane ( ale trzeba od nich odjąć liczbę dwucyfrowych n co są
względnie pierwsze z 980). Te mogę policzyć jako = φ(70) + te dobre z przedziału
71....99
oraz należy odręcznie sprawdzić n≥981( to leci błyskawicznie)
oczywiście φ(980)=φ(22*5*72)=φ(22 )φ(5 )φ(7 )=22−1(2−1)*(5−1)(7−1)
14 lut 22:05
Mila:
No to ja tego nie pamietam, i ile wyszło?
Wiem, że to Mat. Dyskretna.
14 lut 22:10
Mat: uff czyli tak jak napisałam też ok i wyszło 515 , dzięki za pomoc
a czy wielomiany wieżowe zna ktoś ?
16 lut 13:08
 |A∪B∪C|=|A|+|B|+|C|−|A∩B|−|B∩C|−|A∩C|+|A∩B∩C|
|A|−podzielne przez 2
|B|−podzielne przez 7
|C|podzielne przez 5
A potem tak jak napisał Mila
1−|A∪B∪C|
|A∪B∪C|=|A|+|B|+|C|−|A∩B|−|B∩C|−|A∩C|+|A∩B∩C|
|A|−podzielne przez 2
|B|−podzielne przez 7
|C|podzielne przez 5
A potem tak jak napisał Mila
1−|A∪B∪C|
 jak mowicie ze nie ma innego sposobu ....
jak mowicie ze nie ma innego sposobu .... 