 z góry wielkie
dzięki za pomoc
z góry wielkie
dzięki za pomoc 
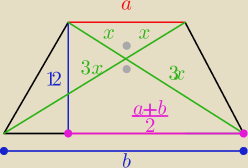 a=x√2
b=3x√2
a=x√2
b=3x√2
| a+b | ||
122+( | )2=(4x)2 | |
| 2 |
| 4x√2 | ||
144+( | )2=16x2 | |
| 2 |
| (6+18)12 | ||
P= | =144 | |
| 2 |
 1/
1/
| 1 | ||
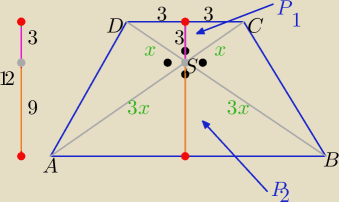
P(tr)= | (9x2+x2+2*3x2)= 8x2 , x= 3√2 | |
| 2 |
 długości podstaw : b=3+3=6 , a=9+9=18
długości podstaw : b=3+3=6 , a=9+9=18
| 6+18 | ||
P(tr)= | *12= 144 [j2] | |
| 2 |

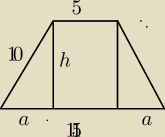 trapez równoraminny o podstawie 5 i 15 a ramionach 10 to rysujemy dwie wysokości tego trapezu
i mamy wtedy do obliczenia pole prostokąta o boku 5 a drugim h i pola dwóch trójkątów
prostokątnych o bokach 10, h , a
to najpierw obliczam a
i z tego zadania wynika ,że 5+2a=15
to 2a=15−5
2a=10/2
a=5
a mając obliczone a obliczam z pitagorasa h:
a2+b2=c2 więć zatem:
a+h=102
h2=52+102
h2=25+100
h2=125
h={125}
h=11,18
więc mając a i h możemy obloczyć pole prostoląta i dwóch trójkątów składających się nz ten
trapez
prostokąt: 5* 11,18=55,75
trójkąt 1/2a*h=p
2,5*11,18=27,97
czyli pole trapezu musi winieść w naszym przypadku sumę pól dwóch trójkątów i prostokąta czyli
55,75 + 27,97 + 27,97 = 111,65
trapez równoraminny o podstawie 5 i 15 a ramionach 10 to rysujemy dwie wysokości tego trapezu
i mamy wtedy do obliczenia pole prostokąta o boku 5 a drugim h i pola dwóch trójkątów
prostokątnych o bokach 10, h , a
to najpierw obliczam a
i z tego zadania wynika ,że 5+2a=15
to 2a=15−5
2a=10/2
a=5
a mając obliczone a obliczam z pitagorasa h:
a2+b2=c2 więć zatem:
a+h=102
h2=52+102
h2=25+100
h2=125
h={125}
h=11,18
więc mając a i h możemy obloczyć pole prostoląta i dwóch trójkątów składających się nz ten
trapez
prostokąt: 5* 11,18=55,75
trójkąt 1/2a*h=p
2,5*11,18=27,97
czyli pole trapezu musi winieść w naszym przypadku sumę pól dwóch trójkątów i prostokąta czyli
55,75 + 27,97 + 27,97 = 111,65
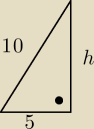 h2=100−25
h2=100−25