zapis funkcji: 0> czy 0)
mic: jest sobie f(x)=|x2−1|−|x2−2x| wiadomo że x=1 x=−1 x=0 x=2
i rysując tę funkcję mam jedną z części(bo trzeba to podzielić na inne) −2x2+2x+1 dla
x∊(−1;0)
moje pytanie to dlaczego nie x∊(−1;0>
7 lut 20:28
asdf: podaj treść zadania całą, przekombinowales i nie zrozumialem pytania

7 lut 20:31
mic: naszkicuj wykres funkcji f(x)=|x2−1|−|x2−2x|
i jak to zrobić,
licząc to wychodzi mi f1(x)= potrafie zrobić
f2(x)=−2x2+2x+1 dla x∊(−1;0> czy dla x∊(−1;0)
f3(x)= potrafie zrobić
f4(x)= potrafie zrobić
7 lut 20:41
asdf:
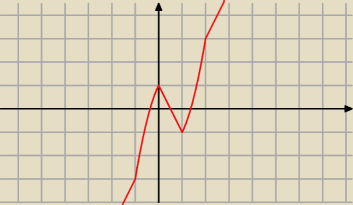

7 lut 20:56
rob: a czy mógłby mi to ktoś wytłumaczyć :
f1(x)= potrafie zrobić
f2(x)=−2x2+2x+1 dla x∊(−1;0> czy dla x∊(−1;0)
f3(x)= potrafie zrobić
f4(x)= potrafie zrobić
7 lut 21:00
asdf: szczerze to nie mam sił

dzisiaj skonczyla mi sie sesja i jestem w stanie wskazujacym...
7 lut 21:06
Ajtek:
asdf cześć. Rozumiem, że oblewasz całkowity sukces

7 lut 21:09
asdf: czesc,ahm
7 lut 21:16
Ajtek:

no to

7 lut 21:17
7 lut 21:18
Ajtek:
Pokaż jak domykałeś inne przedziały.
7 lut 21:20
rob: f1(x)=2x−1 dla x∊(−∞;−1>∪<2;∞)
f2(x)=−2x2+2x+1 dla x∊(−1;0 jaki nawias tu i poniżej
f3(x)=−2x+1 dla x∊ 0;1)
f4(x)=2x2−2x−1 dla x∊<1;2)
7 lut 21:25
Ajtek:
Możesz dać tak:
)
<
Tak samo zrobiłeś poniżej

.
7 lut 21:29
rob: a dlaczego nie:
>
(
rysując oś liczbową wychodzi mi tak jak ja napisałem
np. ile wynosi |x2−1| rysując tą oś wychodzi że −x2+1 dla x∊(−1;1) i x2−1 dla
x∊(−∞;−1>∪<1;∞)
7 lut 21:36
rob: pisząc to; ''np. ile wynosi |x2−1| rysując tą oś wychodzi że −x2+1 dla x∊(−1;1) i x2−1
dla
x∊(−∞;−1>∪<1;∞)''
chciałem pokazać jak ja zrobiłem to swoje zadanie i dlaczego ma nie być
>
(
7 lut 21:37
Ajtek:
Mnie uczono, że domyka się przedziały z lewej strony, jeśli nic tego nie wyklucza.
7 lut 21:40
asdf: 
7 lut 21:45



 dzisiaj skonczyla mi sie sesja i jestem w stanie wskazujacym...
dzisiaj skonczyla mi sie sesja i jestem w stanie wskazujacym...

 no to
no to 




 .
.
