Promień okręgu wpisanego w tójkąt prostokątny

Promień okręgu wpisanego w tójkąt prostokątny Matejko: Promień okręgu wpisanego w trójkąt prostokątny jest równy 2. Tangens jednego z kątów ostrych trójkąta wynosi ³₄. Oblicz odległość między wierzchołkiem kąta prostego a punktem styczności okręgu z przeciwprostokątna. Proszę o podpowiedź

7 lut 18:27

Eta:

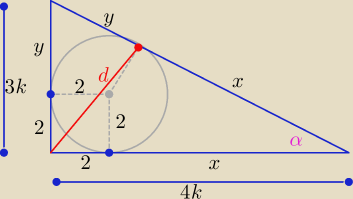
x=4k−2, y=3k−2, k>0 , x+y= √16k²+9k²=5k ⇒ 4k−2+3k−2=5k ⇒ k=2 to: x=6, 4k=8

	3		3
z tw. kosinusów d²= 8²+6²−286*cosα , tgα=		⇒ cosα=
	4		5

d=........ dokończ

7 lut 19:03

Alfa:

	4
Eta, cosα =
	5

7 lut 19:15

Eta: No jasne emotka

dzięki za poprawkę emotka

7 lut 19:23

Matejko: NIE ROZUMIEM tego x+y= pierwiastek z 25k²? dlaczego tak?

8 lut 13:42

Matejko:

8 lut 14:00

Matejko: 16k²+9k² nie czaje tego kompletnie dlaczego tak

8 lut 14:01

Matejko:

8 lut 16:55

MQ: Z tw. Pitagorasa

8 lut 17:03

Matejko: ahaaa a ja patrzyłem na x i y przy przyprostokątnych xd dzięki

8 lut 17:51