Planimetria
czopo: Przekątna trapezu równoramiennego ma długość d i jest nachylona do dłuższej podstawy pod kątem
α. Wykaż, że:
a) pole tego trapezu jest równe 12d2 sin 2α
b) jeżeli w ten trapez można wpisać okrąg to obwód trapezu jest równy 4d cos α
7 lut 17:44
Alfa:
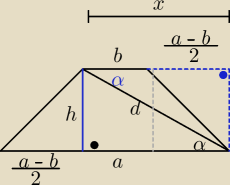
a)
h = dsinα
| | a−b | | 2b+a−b | | a+b | |
x = b + |
| = |
| = |
| |
| | 2 | | 2 | | 2 | |
x = dcosα
więc:
| | 1 | | 1 | |
P = dcosα*dsinα = d2sinαcosα = |
| d2*2*sinαcosα = |
| d2sin2α |
| | 2 | | 2 | |
cbdw
7 lut 18:23
Alfa: b) rys. j/w
zgodnie z tw., jeżeli w ten trapez można wpisać okrąg tzn, że a+b = c + c, czyli a+b = 2c
obwód trapezu, to: L = a+b+2c = a+b+a+b = 2(a+b)
| | a+b | |
a podpunktu a) wiemy, że |
| = dcosα |
| | 2 | |
więc mnożąc obustronnie przez 4 otrzymujemy:
2(a+b) = 4dcosα
zatem:
L = 2(a+b) =
4dcosα
cbdw
7 lut 18:30
 a)
a)