granica = 0? piotrek: lim x→1⁻ √^x−1_1+x jeżeli podstawie 1⁻ w liczniku to wyjdzie 0⁻ pod pierwiastkiem. Czy wtedy granica jest 0⁻, czy powinienem to zrobic inaczej?

Ajtek: Dlaczego liczysz granicę w 1 z lewej strony

Janek191:

	x − 1
Musi być		≥ 0
	1 + x

Tam powinno być

	x − 1
lim x → 1+ √
	1 + x

Janek191: Pomyłka Ma być dodatkowo x ≠ − 1

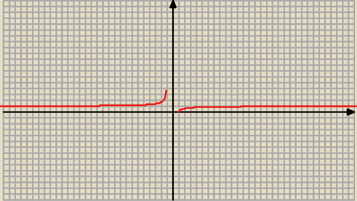
piotrek: Wyznaczam asymptoty tej funkcji. Licze dla 1⁺ i 1⁻, nie wiem czy dobrze. Dziedzina wyszła mi x∊(1, +∞)

Godzio: Asymptoty powinieneś wyznaczać poprzez liczenie granic w −1.

Janek191: Tylko dla 1⁺ czyli > 1 Mniejszych od 1 nie ma !

piotrek: Mimo, że −1 nie należy do funkcji?

Janek191: Asymptota pozioma ma równanie: y = 1

piotrek: Dobrze Janek, a jak chodzi o samą granice z pierwszego postu to pod pierwiastkiem może wyjsc 0⁻

Godzio: Asymptoty liczy się licząc granice przy x → ±∞ i w punktach wykluczonych z dziedziny.

Janek191: Źle określona dziedzina ! Df = < − ∞; − 1 ) ∪ < 1 ; + ∞ )

Janek191:

	x − 1
lim x → −1− √		= +∞
	x + 1

Janek191: Asymptota pionowa ma równanie: x = − 1

Domel: Z dziedziny wynika że nie istnieje granica w 1⁻ bo 1. 1+x≠0 => x≠−1 2. 1−szy układ równań: x−1≥0 => x≥1 1+x≥0 => x≥−1 Z tego wynika, że x≥1 3. 2−gi układ równań: x−1<0 => x<1 1+x<0 => x<−1 Z tego wynika, że x<−1 Z warunków 1, 2 i 3 wynika, że x∊(−∞;−1) ∪ <1;+∞) Więc granica dla 1⁻ nie istnieje