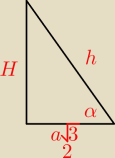
wie bezendu: W ostrosłupie prawidłowym sześciokątnym dany jest kąt nachylenia ściany bocznej do płaszczyzny podstawy α . Oblicz stosunek pola podstawy do pola powierzchni bocznej ostrosłupa. h−wysokość ściany bocznej

	a2√3		3a2√3
Pp=6*		=
	4		2

	a√3		1
cosα=		*
	2		h

	a√3
cosα=
	2h

2hcosα=a√3

	a√3
h=
	2cosα

	a√3
Pb=6*0,5*a*
	2cosα

	3a2√3
Pb=
	2cosα

	Pp		3a2√3		2cosα
k=		=		*
	Pb		2		3a2√3

k=cosα Sorry, że bez rysunku, ale ciężko mam tutaj narysować.

Godzio: Wszystko ok

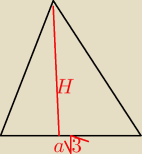
bezendu: Godzio a zobacz to jeszcze jak masz czas. Wysokość prawidłowego ostrosłupa sześciokątnego ma długość H , a krawędź podstawy ma długość a.Wyznacz pole przekroju wyznaczonego przez krótszą przekątną podstawy i wierzchołek ostrosłupa Krótsza przekątna w sześciokącie foremnym ma długość a√3

	1
Pprzekroju=		*a√3*H
	2

	a√3H
Pprzekroju=
	2

?

Godzio: Ale wysokością przekroju nie jest wysokość ostrosłupa, więc póki co jest źle.

bezendu: Dzięki zaraz poprawię

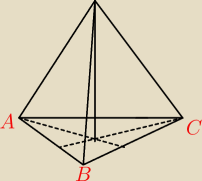
bezendu: Podstawą ostrosłupa jest trójkąt ABC gdzie |AC|=3 |BC|=7 i |∡A|=60. Oblicz objętość tego

	25√3
ostrosłupa jeśli wiadomo, że każda jego krawędź boczna ma długość
	3

7²=3²+x²−2*3*x*cos60⁰ |AB|=8

	7
2R=
	sin600

	7√3
R=
	3

P_p=6√3 H=8√3 V=48j³ ?

bezendu: ?

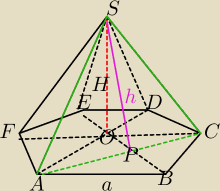
Mila: 00:54 ACS − przekrój h²=|OP|²+H² dokończ

bezendu: Tamto zadanie mam już skończone:

	a√3a2+12H2
Pprzekroju=
	4

bezendu: A zadanie 15:20 ?

Mila: 15:20 mam inna wysokość H

bezendu: Zaraz jeszcze raz przeliczę.

bezendu: H wychodzi 8√3

Mila:

	25√3
H2+R2=		)2
	3

	49*3		625*3
H2+		=
	9		9

	625		49
H2=		−
	3		3

	576
H2=
	3

Dobrze masz, przepraszam.

bezendu: Błąd może zdarzyć się każdemu

bezendu: Mila jesteś jeszcze ?

Mila: Jestem, oglądam otwarcie Olimpiady w Soczi ( Soczi − wspomnienie młodości!).

bezendu: W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej ma długość 4√3 , a ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 60⁰ . Oblicz objętość ostrosłupa V=72√3j³ ?

bezendu: To proszę zajrzy od czasu w chwili przerwy

Mila: Tak. Zgadza sie.

bezendu:

	a2√15
Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego równa się		, gdzie
	4

a oznacza długość krawędzi podstawy tego ostrosłupa. Oblicz cosβ i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość β z dokładnością do 1⁰ P_b=4*0,5ah

	a2√15
2ah=
	4

	a2√15
2ah=
	4

	a2√15		1
h=		*
	4		2a

	√15a
h=
	8

1		a√3
	*
3		2

a√3
6

	a√3		8
cosβ=		*
	6		√15a

	4√3
cosβ=
	3√15

	4√5
cosβ=
	15

zawodus: A co to jest beta?

bezendu: kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy

bezendu: ?

Mila:

	1
Pb=3*		*a*hb
	2

bezendu: Dziękuję.

Mila: Ile?

bezendu:

	√5
cosβ=
	5

Mila: Tak.

bezendu: Objętość ostrosłupa prawidłowego trójkątnego ABCS jest równa 72, a promień okręgu wpisanego w podstawę ABC tego ostrosłupa jest równy 2. Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.

	√3
tg=		?
	9

bezendu: ?

bezendu: Dzięki. Już wiem co źle mam.

Eta: Dobrze masz! To ja źle przeczytałam treść ( kąt nachylenia ściany bocznej)

Mila: Jest dobrze.

Eta: H=6√3, r=2

	2		√3
tgα=		= ......=
	H		9

Eta: No to "spadam"

bezendu: Dziękuję.