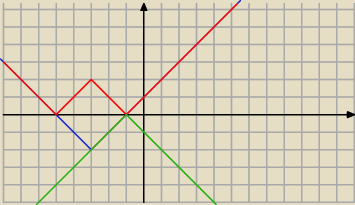
funkcja Radek: Wyznacz te wartości parametru m , dla których równanie ||x + 3| − 2|+ |x +1 | = m ma dokładnie dwa rozwiązania Robię tak że rysuję ||x+3|−2| i potem −|x+1| ale coś nie wychodzi odp z książki ? (−∞,0)suma(2,∞)

Radek: ?

Lorak: Bo zapomniałeś, że po prawej stronie jest jeszcze m −|x+1|+m i trzeba tak dobrać m, żeby były 2 przecięcia.

Radek: ?

Lorak: np. dla m<0 nie będzie rozwiązań dla m=0 będzie jedno pomyśl nad m>0

Godzio: Od siebie proponowałbym narysować funkcję z lewej strony, trochę męczenia, ale do zrobienia

Radek: Nie za bardzo wiem jak ?

Godzio: Zaraz pokaże.

Godzio: f(x) = ||x + 3| − 2|+ |x + 1| Weźmy sobie trzy przypadki: 1^o x ∊ (−∞,−3> f(x) = | − x − 3 − 2| − x − 1 = |x + 5| − x − 1 2^o x ∊ (−3,−1> f(x) = |x + 3 − 2| − x − 1 = |x + 1| − x − 1 = −2x − 2 3^o x ∊ (−1,∞) f(x) = 2x + 2 Pozostaje jeszcze rozbić pierwszy przypadek na dwa przypadki: 1^o a) x ∊ (−∞,−5> f(x) = − 2x − 6 b) x ∊ (−5,−3> f(x) = 4 No to wzór funkcji:

	⎧	− 2x − 6, x∊(−∞,−5>
	⎜	4, x∊(−5,−3>
f(x) =	⎨	− 2x − 2, x∊(−3,−1>
	⎩	2x + 2, x∊(−1,∞)

Radek: Dziękuję ale dla mnie to chyba za trudne.