wartości parametru k nierówność:
Niki: Dla jakich wartości parametru k nierówność:
(k2 − k−6)x2 + 3(k+2)x+1>0 jest prawdziwa dla wszystkich x∊R?
Potrzebuje na teraz!
6 lut 20:54
zawodus: rysunek paraboli jak powinna wyglądać?
6 lut 20:55
Niki: Nie, chodzi o nierównosci kwadratowe
np. przyjać że delta jest mniejsza od 0 żeby leżała nad osia x
imusi wyjść odpowiedż
że x należy (−6;−2>
6 lut 20:59
zawodus:

parabola ma tak wyglądać
jakie do tego warunki?
6 lut 21:00
Niki: no włąśnie nie ma jest tylko ze x ma należeć do R
ale ten wykres moze też być pod osią i też będą rzeczywste ale ujemne, ja nie wiem
6 lut 21:03
Jolanta: ax2+bx+c >0 dla każdego x jeżeli a>0 i Δ <0
6 lut 21:18
Jolanta: k
2−k−6>0 i Δ<0
1 warunek
k
2−k−6>0
Δ=b
2−4ac=1+24=25
rysuje parabole ramiona w góre
nad osia jest przedział k∊(−
∞,−2)v(3,
∞)
2 warunek
Δ>0
6 lut 21:25
Niki: no dalej
6 lut 21:27
zawodus: a czyli czekasz na gotowca?
6 lut 21:28
Jolanta: k2−k−6>0 i Δ <0
1 warunek
k2−k−6>0
Δ=b2−4ac=1+24=25
k1=U{−b−√Δ{2a}=−2
k2=U{−b+√Δ{2a}=3
k∊(−∞,−2)v(3,∞)
2 warunek Δ<0
Δ=
6 lut 21:29
Domel: Czyli:
9(k+2)2−4*(k2−k−6)*1<0
i
k2−k−6>=0
no i trzeba znaleźć wspólny przedział dla tych 2 nierówności
6 lut 21:30
Niki: nom i dalej
6 lut 21:32
Niki: nie czekam na gotowca, patrze jak wy zrobiliscie, bo mi nie wyszło
6 lut 21:33
zawodus: to pokaż jak liczysz...
6 lut 21:34
Niki: ciekawe jak?
z drugiego warunki, z delty k wyszło mi, że
k1 = −6
k2= − 2
i skoro ramiona paraboli w górę, przedział ma zawierac się w liczbach mniejszych od zera
no i wychodzi, że k należy (−6:−2)
no ale z pierwszego warunku wychodzi, że skoro są większe od 0
to sie bierze ten przedział od 3 do + nieskończonosći
ale w odpowiedziach jest że k należy (−6;−2>
tzn, ze gdzieś trzeba postawić warunek mniejszy równy, albo wiekszy równy
ale właśnie nie wiem jak, bo nie chce wyjść
6 lut 21:40
ZKS:
Trzeba rozpatrzeć również warunek kiedy ta funkcja jest funkcją stałą i zobaczyć co się
dostanie.
6 lut 21:41
Niki: napisz mi jak to zrobic, jak ma wygla\DAĆ TEN WARUNEK
6 lut 21:43
Jolanta: przeczytaj co napisałam .w jakich przedziałąch parabola jest nad osią ?
6 lut 21:43
ZKS:
A kiedy funkcją postaci f(x) = ax2 + bx + c jest funkcją stałą (nie jest funkcją kwadratową i
liniową)?
6 lut 21:46
Niki: no właśnie nie wiem
6 lut 21:46
Niki: no tak ale otwary przedział + otwarty nie da zamkniętego
i poza tym jak ten warunek z k był większy od 0 to trzeba chyba wziać ten od 3 do
nieskończonosci
6 lut 21:49
ZKS:
Funkcja postaci f(x) = bx + c jest funkcją kwadratową?
6 lut 21:50
Niki: nie, no ale napisz mi tak jak powinno byc, a nie pytania mi zadajesz
6 lut 21:52
zawodus: czyli liczysz na gotowca...
szkoda bo funkcja liniowa to pierwsza lo
w gimazjum tez coś było o niej...
6 lut 21:53
ZKS:
To teraz pomyśl skoro g(x) = bx + c nie jest funkcją kwadratową to jak zrobić żeby funkcja
f(x) = ax2 + bx + c nie była funkcją kwadratową.
6 lut 21:55
Jolanta: Niki zle myslisz
ta parabola z miejscami zerowymi −2 i 3 ma k >0 tam gdzie jest nad osią czyli w przedziale
(−∞,−2)oraz (3,∞)
6 lut 21:56
Niki: No dobra a bedzie zerem, ale jak niby mam do tego doprowadziC?
6 lut 21:57
Niki: ale to nie zmienia faktu, że przedział wciaż jest otwarty
6 lut 21:58
Jolanta: co ci wyszło z drugiego warunku ?
6 lut 21:59
ZKS:
Skoro a = 0 to zobacz dla jakich k Twoje a będzie równe 0.
6 lut 21:59
Niki: no tak k<−6
ale co z tego?
6 lut 22:01
ZKS:
Dla k < −6 Twoje a = 0? Napisz ile wynosi Twoje a.
6 lut 22:02
Jolanta: ZkS On jeszcze nie skonczył z parabola a Ty o liniową pytasz
6 lut 22:04
Niki: Napiszcie po kolei jak byscie zrobili a nie się migacie
6 lut 22:07
ZKS:
A Ty ją ciągle o to męczysz co sama już zrobiła. Zauważ że pyta się skąd się wziął w odpowiedzi
przedział domknięty z jednej strony.
6 lut 22:07
ZKS:
Napisz ile wynosi Twoje a.
6 lut 22:08
Niki: 0
6 lut 22:10
ZKS:
Twoje a w zadaniu z parametrem.
6 lut 22:10
Niki: 1
6 lut 22:15
ZKS:
Twoja funkcja z zadania wygląda tak
y = 1 * x2 + 3(k + 2)x + 1?
6 lut 22:20
Jolanta: Niki nierównosć bedzie prawdziwa dla wszystkich liczb rzeczywiastych jeżeli wykresem bedzie
parabola leżaca nad osią czyli dla k∊(−6,−2) albo jeżeli to będzie prosta równoległa do osi
OX.
y=ax+b jest wtedy równoległa jeśli a=0
k2−k−6=0 i k+2=0
6 lut 22:22
Niki: k2−k−6
6 lut 22:24
ZKS:
Tutaj się nie zgadzam bo prostą równoległą do osi OX jest też y = −1 a ona jakoś już by nie
spełniała warunków zadania. Musi to być funkcja stała która jest powyżej osi OX.
6 lut 22:26
ZKS:
Okej teraz przyrównuj to do 0.
6 lut 22:27
Niki: pisz po ludzku
rozwiaż mi to jak wiesz
a nie migasz sie
6 lut 22:31
Jolanta: O godz 22;22 napisałam Ci
6 lut 22:34
Niki: wogóle was nie rozumiem
chciałam tylko wiedzieć, co zrobic, zeby ten nawias był domknięty z jednej strony
6 lut 22:35
Jolanta: Rozwiazanie składa sie z paraboli lezacej nad osia i prostej leżacej na osia −funkcja stała
,dlatego tak jest
6 lut 22:37
Niki: a jak ta funkcja stała wygląda?
6 lut 22:37
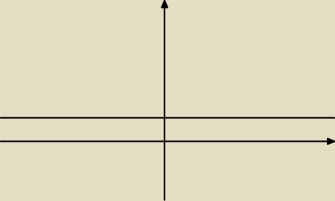
Jolanta:
6 lut 22:38
Jolanta: np y=2x +3 przyjmuje wartosci i ujemne i dodatnie i zero
ale jeżeli zamiast 2 jest 0 to masz y=3 funkcję stałą
dlatego masz przyrównać do zera wszystko co jest przy x
6 lut 22:41
Niki: ale jak ta funkcja ma wyglądać w tym zadaniu, chodzi o równanie
6 lut 22:42
Jolanta: (k2−k−6)x2+3(k−2)x+1>0
K2−k−6=0 i k−2=0 y=1
6 lut 22:45
Niki: i gdzie ten zakmnięty przedział?
6 lut 22:46
Jolanta: jeżeli masz y= ax2+bx+c
i napiszesz warunek a=0 otrzymujesz y=0+bx+c
czyli
funkcje liniową y=bx+c jeżeli napiszesz b=0
otrzymujesz funkcje stała y=c linię równoległa do osi OX
6 lut 22:50
Jolanta: pomyliłam znak k+2=0
k=−2 czyli k∊(−6,2>
6 lut 22:52
Niki: ok
6 lut 22:53
Jolanta: zmeczona jestem k∊(−6 −2>
6 lut 22:53
 parabola ma tak wyglądać
jakie do tego warunki?
parabola ma tak wyglądać
jakie do tego warunki?
