równanie z modułami
stjudent: |x+4|+|8−x| = 16
w pierwszym i trzecim przedziale mi wyszła sprzeczność, w drugim rozwiązanie nie należące do
przedziału
łącznie brak rozwiązań
a za zadanie brak punktów
czemu?
6 lut 20:01
razor: x = −6 lub x = 10
nie wiem jak moglo ci wyjsc brak rozwiazan

6 lut 20:08
stjudent: tak samo na wolphramie wychodzi

ale bez kitu nie mogę do tego dojść
miejsca zerowe to −4 i 8, prawda? te 8−x myli, z x−8 byłoby lajtowo
6 lut 20:12
BlackHawk: jakie przedziały Ci wyszły ?
i podrzuć Twoje rozwiązanie, mi wyszły x=−6 i x=10
Jakim cudem sprzeczne Ci wyszły ?
6 lut 20:12
BlackHawk: jakie przedziały Ci wyszły ?
i podrzuć Twoje rozwiązanie, mi wyszły x=−6 i x=10
Jakim cudem sprzeczne Ci wyszły ?
dla x∊(−∞;−4) dla x∊<−4;8) dla x∊<8,∞)
−x−4+8−x=16 x+4−8+x=16 x+4−8+x=16
−2x=16 2x=20 2x=20
x=−6 x=10 x=10
do swojego przedziału nie należy tylko wynik środkowy ...
6 lut 20:12
PW: Tak, najlepszą metodą rozwiązywania równań jest:
a) zgadnąć rozwiązania
b) wykazać, że innych nie ma.
W ten sposób zabijasz śmiechem autora, któremu wydawało się, że wymyślił trudne zadanie.
6 lut 20:13
BlackHawk: spójrz na moje rozwiązania ....
jak coś nie jasne to pytaj .
6 lut 20:13
Jolanta: 1 przedział
(−∞,−4) −x+4−x=16
2
<−4,8) x+4+8−x=16
3
<8,∞) x+4−8+x=16
6 lut 20:15
Mila:
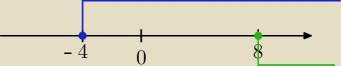
|x+4|+|8−x| = 16 ⇔
|x+4|+|x−8|=16
|x+4|=x+4 dla x+4≥0⇔x≥−4
|x−8|=x−8 dla x−8≥0⇔x≥8
Zaznaczam na osi te przedziały w których wyrażenia (x+4), (x−8) są nieujemne.
1)x<−4
−x−4−x+8=16
−2x=12
x=−6 ∊D
2) x≥−4 i x<8
x+4−x+8=16 ⇔12=16 sprzeczność brak rozwiązań
3) x≥8
x+4+x−8=16
2x=20
x=10∊D
odp.
x∊{−6,10}
6 lut 20:15
BlackHawk: fakt, środkowe równanie u mnie powinno być x+4+8−x=16
źle rozpisałem przez pośpiech. ale to oczywiście jest sprzeczne.
6 lut 20:19
stjudent: zrozumiałem to na swó sposób, ale czemu 8−x be, a x−8 ok?
6 lut 20:27
Jolanta: najpierw wyznaczasz przedziały ,póżniej bierzesz jakąs liczbę z przedziału i patrzysz jaki
wynik wychodzi.Jeśli dodatni nie zmieniasz znaków,jeśli ujemny zmieniasz.A póżniej
rozwiazujesz
6 lut 20:30
Eta:
|8−x|= |−(x−8)|= |x−8|
6 lut 20:31
Mila:
|x−8|=|8−x|
Latwiej liczyc dla wariantu |x−8|.
6 lut 20:32
PW: I tu mamy piękny przykład jak zastosować interpretację geometryczną wartości bezwzględnej.
Widzimy na osi dwa punkty: −4 i 8.
Symbol |x+4| oznacza odległość punktu x od punktu (−4).
Symbol |8−x| = |x−8| oznacza odległość punktu x od punktu 8.
Żaden punkt z przedziału [−4,8] nie jest rozwiązaniem, gdyż suma jego odległości od −4 i od 8
jest równa 12.
Zgadłem rozwiązanie z przedziału (−
∞, −4) − to liczba (−6). Innego rozwiązania w tym przedziale
nie ma, bo gdy punkt przesuwa się w lewo w tym przedziale, wzrastają obie odległości, a gdy
przesuwa się w prawo − obie odległości maleją.
Zgadłem rozwiązanie z przedziału (8,
∞) − jest to liczba 10. Innych rozwiązań w tym przedziale
nie ma, bo ...

6 lut 20:48

 ale bez kitu nie mogę do tego dojść
miejsca zerowe to −4 i 8, prawda? te 8−x myli, z x−8 byłoby lajtowo
ale bez kitu nie mogę do tego dojść
miejsca zerowe to −4 i 8, prawda? te 8−x myli, z x−8 byłoby lajtowo
 |x+4|+|8−x| = 16 ⇔
|x+4|+|x−8|=16
|x+4|=x+4 dla x+4≥0⇔x≥−4
|x−8|=x−8 dla x−8≥0⇔x≥8
Zaznaczam na osi te przedziały w których wyrażenia (x+4), (x−8) są nieujemne.
1)x<−4
−x−4−x+8=16
−2x=12
x=−6 ∊D
2) x≥−4 i x<8
x+4−x+8=16 ⇔12=16 sprzeczność brak rozwiązań
3) x≥8
x+4+x−8=16
2x=20
x=10∊D
odp.
x∊{−6,10}
|x+4|+|8−x| = 16 ⇔
|x+4|+|x−8|=16
|x+4|=x+4 dla x+4≥0⇔x≥−4
|x−8|=x−8 dla x−8≥0⇔x≥8
Zaznaczam na osi te przedziały w których wyrażenia (x+4), (x−8) są nieujemne.
1)x<−4
−x−4−x+8=16
−2x=12
x=−6 ∊D
2) x≥−4 i x<8
x+4−x+8=16 ⇔12=16 sprzeczność brak rozwiązań
3) x≥8
x+4+x−8=16
2x=20
x=10∊D
odp.
x∊{−6,10}
