bryły
bezendu:
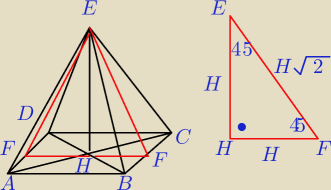
W ostrosłupie prawidłowym czworokątnym wysokości przeciwległych ścian bocznych, poprowadzone z
wierzchołka ostrosłupa, są do siebie prostopadłe.
Oblicz sinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Dobrze to zacząłem ?
6 lut 19:22
bezendu:
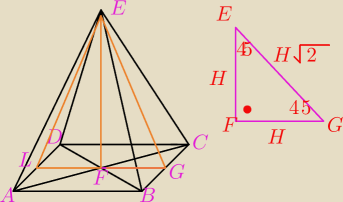
Jeszcze raz tylko inne oznaczenia ?
Z trójkąta ΔEGC policzyłem |EC|=
√3h
|FG|−połowa przekątnej podstawy czyli H
√2
?
6 lut 19:35
Hajtowy:
Widzę, że coś z rozszerzenia rzuciłeś

a
2=c
2+c
2
Pitagoras w trójkącie AFE
c=...
Później trójkąt prostokątny EFI
H=...
No i później sinus kąta.
Taka jest moja teoria spiskowa tego zadania − gościa z podstawy

6 lut 19:38
bezendu:
To jest zadania z podstawy a nie R

6 lut 19:39
Hajtowy:
Nie wiem czy to dobrze, bo ja z brył to cienias jestem

6 lut 19:40
Hajtowy: bezendu podst, czy R −> Bryły to koszmar

6 lut 19:41
bezendu:
Już coraz mniejszy ten koszmar, ale na początku tragedia.
6 lut 19:42
Hajtowy: a
2=b
2+b
2
| | a√2 | |
b2= |
|  Walnąłem się na symbolach... ale wtopa  |
| | 2 | |
6 lut 19:42
bezendu: ?
6 lut 19:54
zawodus: Geometria 3D nie jest taka trudna

6 lut 20:00
bezendu: Ale czy rozwiązanie ok ?
6 lut 20:04
Hajtowy: zawodus, jakie jest rozwiązanie?

6 lut 20:05
Mila:
Napisałeś cosinus zamiast sinus. Bardzo komplikujesz te obliczenia.
| | | |
sin∡FBE= |
| =abyś się nie pomylił, to zapisz tak: |
| | | |
| | 1 | | 2 | | 1 | | √3 | |
= |
| a* |
| = |
| = |
| |
| | 2 | | a√3 | | √3 | | 3 | |
6 lut 20:06
bezendu:
Nie mam jeszcze wprawy, i dlatego..
6 lut 20:07
bezendu: Dziękuję Mila idę robić następne.
6 lut 20:09
zawodus: O wyszedłem na chwilę i już rozwiązanie jest

6 lut 20:11
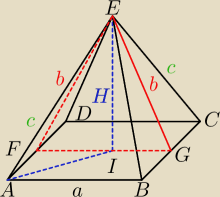
Mila:
Bezendu stosuj ogólnie przyjęte oznaczenia:
6 lut 20:19
zawodus: na szczęście za to nie odejmują punktów

6 lut 20:21
bezendu: Dobrze, ja zawsze oznaczam krawędź podstawy a ale miałem tam trójkąt równoramienny i
uzależniłem wszystko od H ostrosłupa.
6 lut 20:21
Mila:
Zauważyłam.
Dalej rozwiązuj.
6 lut 20:23
bezendu:
Kąt płaski ściany bocznej przy wierzchołku ostrosłupa prawidłowego czworokątnego ?
Może ktoś narysować ten kąt ?
6 lut 20:28
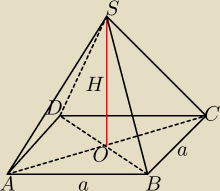
Mila:
to np. kąt BSC rys 20:19
6 lut 20:30
zawodus: Ściana boczna to trójkąt

Szukasz kąta przy wierzchołku

Czyli tak jak podała Mila

6 lut 20:33
bezendu: W graniastosłupie czworokątnym prawidłowym przekątna o długości m jest nachylona do
płaszczyzny podstawy pod kątem α . Wiadomo, że sin α = 0,2 . Wyznacz objętość tego
graniastosłupa
6 lut 21:10
zawodus: nie ma odpowiedzi w książce?

6 lut 21:12
Mila:
Wynik prawidłowy.
Jak liczyłes pole podstawy?
6 lut 21:14
bezendu:
Mam zadania na kartce od Pani do zrobienia.. A jest ich ponad 200. Odpowiedzi będę znał po
feriach a to za późno dla mnie, bo ja muszę wiedzieć czy dobrze robię te zadania.
6 lut 21:15
Hajtowy: | | 12 | |
bezendu gites  V= |
| m 3  |
| | 125 | |
6 lut 21:15
bezendu:
| | H | |
Najpierw zrobiłem 0,2= |
| ⇒ H=0,2m |
| | m | |
| | 2√6 | |
Wyliczyłem długość przekątnej podstawy |
| m |
| | 5 | |
| | 2√6 | |
i ze wzoru na długość przekątnej a√2= |
| m wyznaczyłem a. |
| | 5 | |
6 lut 21:18
Mila:
Tak myślałam. Ułatwienie (mniej obliczeń, mniej okazji do popełnienia błędu)
| | 24 | |
p2= |
| m2 z tw.Pitagorasa. |
| | 25 | |
| | 1 | | 12 | |
P{kwadratu}= |
| p2= |
| m2 |
| | 2 | | 25 | |
6 lut 21:43
bezendu: Bardzo dziękuję za te sposoby, będę analizował..
6 lut 21:55
bezendu:
I tutaj się zaciąłem :
Odległość środka podstawy ostrosłupa prawidłowego czworokątnego od krawędzi bocznej równa się
a, a kąt płaski ściany bocznej przy wierzchołku ostrosłupa równa się 2α . Oblicz wysokość
ostrosłupa.
Proszę o naprowadzenie.
6 lut 22:00
zawodus: rysunek masz?
6 lut 22:05
bezendu: Mam, ale nic z niego nie mogę odczytać tylko a.
6 lut 22:07
zawodus:
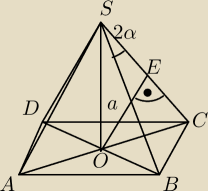
rysunek

idzie mi coraz lepiej

6 lut 22:11
Aga1.:
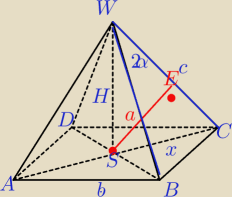
6 lut 22:11
bezendu:
Czemu ta odległość jest |SE| a nie |SC| ?
6 lut 22:13
zawodus: A jak się oblicza odległość punkt od prostej?
6 lut 22:15
bezendu:
Ze wzoru. d=..
6 lut 22:16
zawodus: Masz prostą i punkt co robisz aby obliczyć odległość tego punktu od prostej? Jak byś miał
wykonać rysunek?
6 lut 22:19
bezendu:
Prowadzę prostą prostopadłą do tej prostej która przechodzi przez ten punkt.
6 lut 22:22
Aga1.:
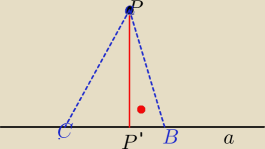
Odległość punktu P od prostej a to długość odcinka PP
' nie PB, czy PC
6 lut 22:22
zawodus: Dobrze, a teraz odpowiedz sobie na swoje pytanie dlaczego?
czy odcinek SC jest prostopadły do WC?

6 lut 22:25
bezendu: Tylko co dalej zrobić ?
6 lut 22:26
zawodus:
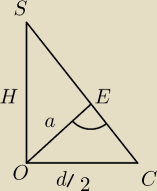
Brakuje ci jeszcze boku OC lub SC. Myśl jak wyznaczyć jeden z nich.
6 lut 22:31
bezendu:
Chyba już wiem

6 lut 22:44
zawodus: 
6 lut 22:45
Mila:
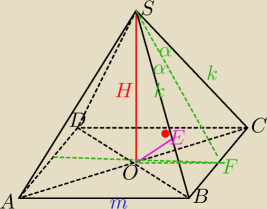
OE⊥SB
|OE|=a
W ΔSFB:
|BF|=k*sinα
m=2k sinα
| | 1 | | 1 | |
|OB|= |
| m√2= |
| *2ksinα*√2=√2ksinα |
| | 2 | | 2 | |
Teraz oblicz pole ΔSOB na dwa sposoby.
OE jest wysokością opuszczona na SB
6 lut 22:46
bezendu: Na dwa sposoby ?
6 lut 22:51
zawodus: podstawa + wysokość
podstawa + wysokość
za każdym razem inne.
6 lut 22:53
Mila:
Tak, to jest Δ prostokątny.
6 lut 22:55
bezendu: Dziękuję jutro do tego wrócę bo nie do końca to zrozumiałem.
6 lut 23:01
Mila:
6 lut 23:08
bezendu:
Ale ja jeszcze analizuję 22:46
6 lut 23:09
Mila:
Powodzenia. Dobranoc

6 lut 23:12
bezendu: I tak będę siedział do 03:00 ale wiem,że Ty już idziesz. Dobranoc i dziękuję.
6 lut 23:13
bezendu: Jest jeszcze jakiś inny sposób na to zadanie ?
7 lut 20:28
Mila:
Jest, Δpodobne, podany jest łatwiejszy.
cd. 22:46
| | 1 | | 1 | |
PΔSOB= |
| *|SB|*d= |
| *|OB|*H⇔ |
| | 2 | | 2 | |
√2*sinα*H=d
7 lut 20:50
bezendu: Dziękuję.
7 lut 21:06
 W ostrosłupie prawidłowym czworokątnym wysokości przeciwległych ścian bocznych, poprowadzone z
wierzchołka ostrosłupa, są do siebie prostopadłe.
Oblicz sinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Dobrze to zacząłem ?
W ostrosłupie prawidłowym czworokątnym wysokości przeciwległych ścian bocznych, poprowadzone z
wierzchołka ostrosłupa, są do siebie prostopadłe.
Oblicz sinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Dobrze to zacząłem ?
 Jeszcze raz tylko inne oznaczenia ?
Z trójkąta ΔEGC policzyłem |EC|=√3h
|FG|−połowa przekątnej podstawy czyli H√2
Jeszcze raz tylko inne oznaczenia ?
Z trójkąta ΔEGC policzyłem |EC|=√3h
|FG|−połowa przekątnej podstawy czyli H√2
 Widzę, że coś z rozszerzenia rzuciłeś
Widzę, że coś z rozszerzenia rzuciłeś  a2=c2+c2
a2=c2+c2




 Walnąłem się na symbolach... ale wtopa
Walnąłem się na symbolach... ale wtopa 



 Bezendu stosuj ogólnie przyjęte oznaczenia:
Bezendu stosuj ogólnie przyjęte oznaczenia:

 Szukasz kąta przy wierzchołku
Szukasz kąta przy wierzchołku  Czyli tak jak podała Mila
Czyli tak jak podała Mila 

 V=
V=
 rysunek
rysunek  idzie mi coraz lepiej
idzie mi coraz lepiej 

 Odległość punktu P od prostej a to długość odcinka PP' nie PB, czy PC
Odległość punktu P od prostej a to długość odcinka PP' nie PB, czy PC

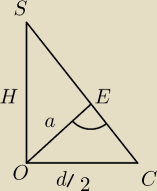 Brakuje ci jeszcze boku OC lub SC. Myśl jak wyznaczyć jeden z nich.
Brakuje ci jeszcze boku OC lub SC. Myśl jak wyznaczyć jeden z nich.


 OE⊥SB
|OE|=a
W ΔSFB:
OE⊥SB
|OE|=a
W ΔSFB:

