wo
Radek:
Wielomian W (x) przy dzieleniu przez dwumiany (x − 1),(x + 2),(x − 3 ) daje reszty
odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian P (x) =
x3 − 2x2 − 5x+ 6 .
Proszę o wytłumaczenie bo mam jeszcze problem z tymi zadaniami.
6 lut 15:51
Mila:
1) najpierw sprawdź jakie pierwiastki ma wielomian P(x).
6 lut 15:54
Radek:
P(x)=(x−1)(x+2)(x−3)
6 lut 16:04
Saizou :
weźmy przykład na liczbach
7:3=2 r.1 zatem 7=3*2+1
i przerzuć to na wielomiany xd
6 lut 16:05
zawodus: W(x)=P(x)*Q(x)+R(x)
W(x)=(x−1)(x+2)(x−3)*Q(x)+ax
2+bx+c
Teraz liczysz:
W(1), W(−2), W(3)

6 lut 16:08
Mila:
W(x)=(x−1)*(x+2)*(x−3)*Q(x)+R(x)
Reszta z dzielenia W(x) przez P(x) ma postać:
R(x)=ax2+bx+c
R(1)=5
R(−2)=2
R(3)=27
Utwórz układ 3 równań z 3 niewiadomymi: a,b,c
6 lut 16:11
Radek: Dziękuję.
6 lut 16:15
Mila: 
6 lut 16:22
Radek: A mogę jeszcze Panią prosić o pomoc w kilku zadaniach ?
6 lut 16:31
Mila:
Naturalnie, ale czekaj cierpliwie na podpowiedź, bo odchodzę od komputera co kilka minut.
6 lut 16:33
Radek: Pytam bo ostatnio się chyba Pani na mnie zdenerwowała w tym temacie wartości bez

6 lut 16:35
Mila:
Radek , nigdy nie denerwuję się na ucznia z powodu jego trudności w zrozumieniu.
Moze mnie tylko zdenerwować niegrzeczny komentarz, ale wtedy daną osobe ignoruję, omijam z
daleka.
Masz wątpliwości, pytaj . Czasem warto zostawic problem i do niego wrócic na drugi czy piąty
dzien.
Powodzenia w dalszych zmaganiach.
6 lut 17:06
Radek: Dziękuję.

6 lut 17:06
Radek:
Jak graficznie rozwiązać taki układ
{ x2−6x=7+2y−y
|y−1|=x+2.
(x−3)2+(y−1)2=17
S=(3,1) r=√17
Tego drugiego nie wiem kompletnie.
6 lut 17:53
52: |y−1|=x+2
y−1=x+2 v y−1=−x−2
y=x+3 v y=−x−1
dla y>1 dla y<1
Tak myślę ...
6 lut 17:56
Radek: Wiem jak rozpatrzeć ale nie wiem jak to narysować jak mam w module y ?
6 lut 17:59
Mila:
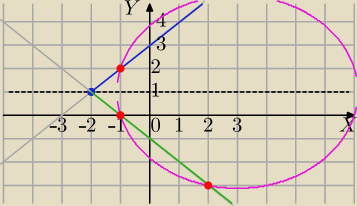
|y−1|=x+2 ⇔x+2≥0⇔x≥−2
1) |y−1|=y−1 dla y−1≥0⇔y≥1
wtedy mamy równanie:
y−1=x+2 i x≥−2
y=x+3 i y≥1 i x≥−2
2) |y−1|=−y+1 dla y<1 i x≥−2
−y+1=x+2
y=−x−1 i y<1 i x≥−2
rozw.
(−1,0),(−1,2), (2,−3),(2,5)
6 lut 18:16
Radek:
Normalnie rysować te proste bez przedziałów ?
6 lut 18:21
Mila:
No nie całkiem , popatrz jakie dałam ograniczenia .
Niebieska nad prostą y=1 i x≥−2 półprosta
Zielona pod prostą y=1 i x≥−2
6 lut 18:26
ZKS:
Aby narysować wykres |y − 1| = x + 2 dajemy najpierw założenie x + 2 ≥ 0 ⇒ x ≥ −2.
Teraz rozbijamy wartość bezwzględną.
|y − 1| = x + 2
y − 1 = x + 2 ∨ y − 1 = −x − 2
y = x + 3 ∨ y = −x − 1.
Rysujesz te dwie proste dla x ≥ −2.
Zobacz wykresy które narysowała
Mila.

6 lut 18:30
Radek:
A mogę prosić o jakiś przykład, żebym ja teraz sam coś podobnego naszkicował ?
6 lut 18:31
ZKS:
Oczywiście nie proste tylko półproste jak pisze
Mila.

6 lut 18:31
ZKS:
Sam możesz sobie nawet wymyślić tylko pozmieniaj sobie liczby.
6 lut 18:32
Mila:
(x−3)2+(y−1)2=17
|y−1|=x−2
6 lut 18:34
Radek:
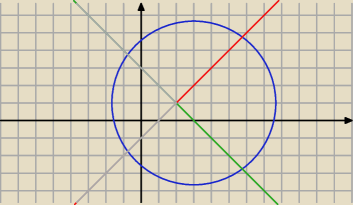
Tak ?
6 lut 18:39
Mila:
W porządku, widzisz, że bez założeń byłyby 4 rozwiązania, a są tylko dwa.
6 lut 18:42
Radek: A jeszcze mam pytanie Pani podaje założenia jeszcze odnośnie x
a ja w module mam tylko y ?
6 lut 18:44
ZKS:
A widziałeś żeby modułu przyjął wartość ujemną? Dlatego trzeba dawać założenia na x aby
wartości te były nieujemne.
6 lut 18:57




 |y−1|=x+2 ⇔x+2≥0⇔x≥−2
1) |y−1|=y−1 dla y−1≥0⇔y≥1
wtedy mamy równanie:
y−1=x+2 i x≥−2
y=x+3 i y≥1 i x≥−2
2) |y−1|=−y+1 dla y<1 i x≥−2
−y+1=x+2
y=−x−1 i y<1 i x≥−2
rozw.
(−1,0),(−1,2), (2,−3),(2,5)
|y−1|=x+2 ⇔x+2≥0⇔x≥−2
1) |y−1|=y−1 dla y−1≥0⇔y≥1
wtedy mamy równanie:
y−1=x+2 i x≥−2
y=x+3 i y≥1 i x≥−2
2) |y−1|=−y+1 dla y<1 i x≥−2
−y+1=x+2
y=−x−1 i y<1 i x≥−2
rozw.
(−1,0),(−1,2), (2,−3),(2,5)


 Tak ?
Tak ?