miary kątów w trójkącia dziś : mam trójkąt ABC. A=(0,0) B=(7,0) C=(2,5) W zadaniu mam wyznaczyć równania prostych zawierających boki trójkąta, środkowe trójkąta i symetralne oraz środek, promień i równanie okręgu opisanego, ortocentrum, środek ciężkości, obwód, pole. Wszystko to juz obliczyłam. Ale w następnym punkcie zadania mam wyznaczyć miary kątów z dokładnością do sekundy kątowej. Jak to zrobić, mając dane, które wcześniej wyznaczyłam?

wredulus: Masz wspolczynniki kierunkowe prostych zawierajacych dane boki ... wspolczynnik kierunkowy prostej =tg (kata nachylenia tej prostej do osi OX)

dziś: prosta zawierająca bok AB to y=0, więc jaki jest jej współczynnik?

wredulus: Zauwaz ze ta prosta jest prostopadla do osi OX ... kat jaki tworzy z OX to 90^o

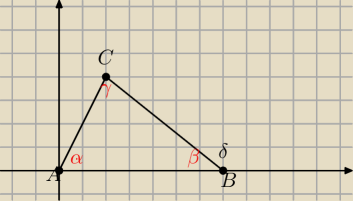
Aga1.: Ten trójkąt nie jest prostokątny

dziś : ale jak to się ma do miary kątów tego trójkąta? przecież to nie jest trójkąt prostokątny...

dziś: pomoże ktoś

dziś: i jak mając te dane wyznaczyć długość wysokości trójkąta?

Aga1.: tgα=a_prostejAB i z tablic odczytujesz wartość kąta α z daną dokładnością. tgδ=a_{prostej BC} β=180⁰−δ

Aga1.: Pole obliczyłabym ze wzoru Herona lub z wyznacznika pary wektorów Wysokości liczyłabym ze wzoru na pole trójkąta

dziś: ale ja właśnie nie wiem jakie jest a prostej AB

J: Prosta AB to jest oś OX,czyli równanie prostej: f(x) = 0 wspóczynnik a = 0 , tg0^o = 0

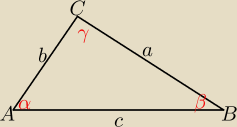
Bogdan: jest kilka sposobów na wyznaczenie miar kątów, np. z twierdzenia cosinusów:

	b2 + c2 − a2
cosα =
	2bc

	a2 + c2 − b2
cosβ =
	2ac

	a2 + b2 − c2
cosγ =
	2ab

W tym zadaniu: a² = 50, b² = 29, c² = 49,

	29 + 49 − 50
cosα =		≈ 0,3713906764 = cos68o11'55''
	2*√29√49

α = 68^o11'55'' Pozostałe miary kątów oblicza się tak samo. Można mając długość promienia okręgu opisanego R skorzystać z twierdzenia sinusów.

	a
sinα =
	2R

	2P
Mając wartość pola P można skorzystać z sinα =
	bc

Są jeszcze inne sposoby

dziś: Bogdan, wielkie dzięki! mam jeszcze jedno pytanie co do tego: wyliczałam to z twierdzenia sinusów. i np. sinα=0,9290 i jeszcze jakieś liczby po przecinku. W tablicach z wartościami funkcji najbliżej tej wartości odpowiada kąt 68 stopni, ale nie jest to dokładnie ta wartość. Więc jak z tego wyliczyć sekundy i minuty?

Bogdan: Zadajmy to pytanie maturzystom. Jeśli sinα = 0.9284766908852593, to α = ? Wynik trzeba podać z dokładnością do sekundy. Jeśli nikt nie odpowie, to wyjaśnię sposób wyznaczania wartości miary kąta

Bogdan: Nikt nie odpowiedział, więc wyjaśniam. sinα = 0.9284766908852593 I sposób. Bierzemy dokładne tablice wartości funkcji trygonometrycznych (nie maturalne) i odczytujemy wynik. II sposób. Na kalkulatorze wciskamy przycisk asin lub sin⁻¹, wpisujemy 0.9284766908852593 i otrzymujemy wynik. Jeśli kalkulator jest nastawiony na radiany, to postępujemy następująco: sin⁻¹ 0.9284766908852593 = 1.190289949682531732927733775 [radianów] 180^o = 648000''

	648000*1.190289949682531732927733775
α =		= 245514,9258491334776271184821
	π

α ≈ 245515''

	245515''		55
		= (4091		)' = 4091'55''
	60		60

	4091'		11
		= (68		)o = 68o11'
	60		60

Ostatecznie α = 68^o11'55'' Można również posłużyć się arkuszami kalkulacyjnymi