1333 qu: Przekrój osiowy stożka jest trójkątem równobocznym o polu 18. Oblicz pole powierzchni bocznej tego stożka.

zawodus: w czym problem?

exevan:

	a2 √3
P=		− wzór na trójkąt równoboczny
	4

	a2 √3
18=		/ *4
	4

72=a² √3 / : √3

72
	=a2
√3

24√3=a² a=√4*3√3 a=2√6√3 a=2*3√2 a=6√2 Pb = πrl

	a
r=
	2

r=3√2 l=a l=6√2 Pb=π*3√2*6√2 Pb=36π Jeśli się pomyliłem to proszę poprawić

qu: jak obliczam a to wychodzi mi ze wzoru na pole trójkąta równobocznego a²= 24√3 czyli a wyjdzie pierwiastek z pierwiastka. Chyba ze zła mam metode

qu: powinno wyjść 12√3π

bezendu: Źle Ci wyszło....

bezendu: P_b=πrl

	1
r=		a
	2

	1
Pb=π*		a*a
	2

	a2π
Pb=
	2

	24√3π
Pb=
	2

P_b=12√3π

qu: wszystko sie poskracało elegancko, dzięki

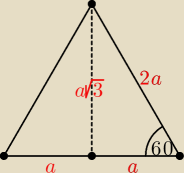
Bogdan: Korzystamy z własności trójkąta prostokątnego o kącie ostrym 60^o P_B = π*a*2a = 2πa²

	2π√3
Pole trójkąta P = 18 ⇒ a*a√3 = 18 /*		⇒ PB = 12π√3
	3