Oblicz Magda: Oblicz objętość ostrosłupa prawidłowego czworokątnego, którego ściana boczna ma wysokość h i jest nachylona do podstawy pod kątem \alpha

dero2005:

a   2
	= cosα
h

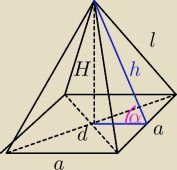
a = 2hcosα

H
	= sinα
h

H= hsinα

	a2H		4
V =		=		h3sinαcos2α
	3		3

bezendu:

	|FG|
h=
	sin(90−α)

	|FG|
h=
	cosα

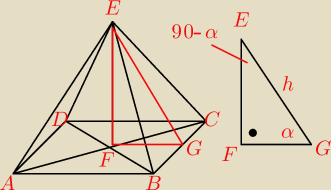
|FG|=hcosα P_p=(2hcosα)² P_p=4h²cos²α |EF|²=h²−|FG|² |EF|²=h²−(hcosα)² |EF|²=h²−h²cos²α |EF|²=h²(1−2cos²α) |EF|=h√1−2cos²a

	1
V=		*4h2cosα*h√1−2cos2α
	3

	4h3√1−2cos2αcosα
V=
	3

Magda: dzięki wielkie

zawodus: bezendu niepotrzebnie u ciebie we wzorze 2cos²α

zawodus: ta dwójka jest źle (jej po prostu tam nie ma)

bezendu: w której linijce ?

zawodus: 4 od dołu

Mila: Bezendu masz tam błąd, coś źle zobaczyłeś, bo wcześniej ładnie. Powinno być po wyłączeniu h² |EF|²=h²(1−cos²α)=h²sin²α |EF|=h sinα

	1
V=		*4h2cos2α*h*sinα
	3

	4h3sinα cos2α
V=
	3

bezendu: poprawiam: |EF|²=h²(1−cos²α) |EF|=h√1−cos²α

	1
V=		*4h2cosα2*h√1−cos2α
	3

	4h3cos2√1−cos2α
V=
	3

bezendu: Zaraz dojdę do rozwiązania Mili

	4h3cos2√sin2α+cos2α−cos2α
V=
	3

	4h3cos2√sin2α
V=
	3

	4h3cos2sinα
V=
	3

Czyli wyszło ok, ale czy ta wersja z 20:56 też by się nadała na ostateczny wynik ?

Mila: Mogła by być, w cos² brak α ,ale wszyscy by się zdziwili, że nie wiesz jak inaczej zapisac (1 − cos²α)

bezendu: W sumie najprostsza postać to ta którą Ty podałaś. Głupie pytanie z mojej strony. Dziękuję.

Mila: Wcale nie głupie pytanie. Masz rozwiać wszystkie wątpliwości.