123 qu: Wśród stożków o sumie długości wysokości i tworzącej równej 6 dm znajdź ten, który ma największa objętość.

zawodus: No to piszesz wzór na objętość stożka.

qu: V= 1/3 π r² h h+l=6 nie wiem jak r wyznaczyć

Mila:

	1
V=		*πR2*h
	3

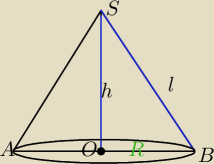
h+l=6 l=6−h, h<6 l²=h²+R² R²=l²−h² R²=(6−h)²−h² R²=36−12h

	1
V=		*π*(36−12h)*h
	3

	π
V=		(36h−12h2) funkcja ma maksimum w wierzchołku paraboli
	3

	−36		3
hw=		=
	−24		2

	3
h=
	2

	π		3		3
V=		(36*		−12*(		)2) oblicz
	3		2		2

	3
l=6−		=4,5
	2

	3
R2=36−12*		=36−18=18
	2

R=3√2

qu: Dziękować

Mila:

qu: obliczyłem chyba trochę inaczej r i wyszło 6 pierwiastek z 2 r² = l²−h² 4,5² − 1,5²= 81/4 − 9/4 = 72/4= 6√2 gdzieś jest błąd ?

Mila: 72:4=18 r=√18=√9*2=3√2

qu: jak zwykle w najprostszych obliczeniach błąd.

Mila: Zdarza się.