...
mati:
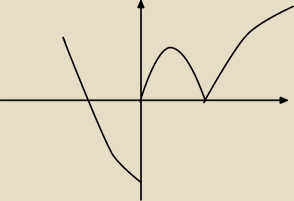
Czy tak może wyglądać wykres :
f'(x)<0 dla x<0 , f'(x)>0 dla x>0 , f''(x)<0 dla x∊(0,2) i punkt przegięcia f(2)=0
5 lut 19:56
Lopo: Może − przecież dla każdego x przyporządkowuje jeden y, nie więcej
5 lut 21:56
mati: czyli nie konieczne jest zeby ten wykres łączył sie z tą częścią gdzie x<0 ?
5 lut 22:28
PW: Po prostu funkcja jest nieciągła w zerze (albo zero nie należy do dziedziny). Z tego rysunku
nie można odczytać właściwej odpowiedzi, ale sądząc po napisach pod wykresem można
wywnioskować, że 0 nie należy do dziedziny
5 lut 22:39
mati: a jakby x należał do R to wtedy funkcja musiałaby być ciągła ?
6 lut 11:08
wredulus_pospolitus:
Nie ... nie może tak wyglądać
6 lut 11:11
wredulus_pospolitus:
skoro f'(x) > 0 dla x>0 ... to funkcja f(x) NIE MOŻE MALEĆ na prawo od osi OY ... a maleje
dla x0 = 2 mamy PUNKT PRZEGIĘCIA a nie ekstremum
6 lut 11:12
mati: nie może dla takich warunkow początkowych jak napisałem ?
6 lut 11:12
Ajtek:
Nie. Dla x∊R funkcja w punkcie x0 nie musi być ciągła, czyli w punkcie x0 ma różne granice.
limx→x0− f(x)=a i limx→x0+ f(x)=b i a≠b oznacza, że f(x) w punkcie x0 nie jest
ciągła.
Wygląda to mniej więcej tak jak na Twoim rysunku dla x=0
6 lut 11:13
mati: a mógłbyć mi jakoś w przybliżeniu to narysować ?
6 lut 11:13
Ajtek:
Cześć
wredulus, ale długo to pisałem
.
6 lut 11:14
wredulus_pospolitus:
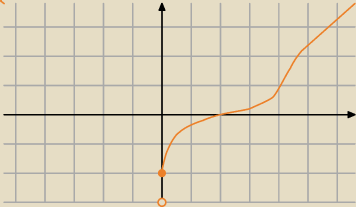
np. tak
tylko w x
0=2 masz wyraźny punkt przegięcia (nie widać tego na rysunku)
6 lut 11:16
wredulus_pospolitus:
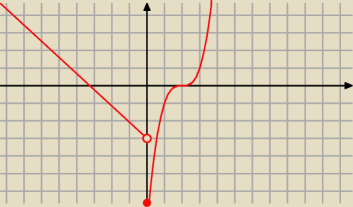
teraz trochę lepiej to wygląda
6 lut 11:18
mati: a te punkty na osi y mogę brać dowolne ?
6 lut 11:19
wredulus_pospolitus:
mogą być dowolne ... istotne jest aby:
1) na lewo od osi OY funkcja ZAWSZE MALAŁA
2) na prawo od osi OY funkcja ZAWSZE rosła
3) aby w (2,0) był punkt przegięcia (np. tak jak na rysunku)
w x=0 funkcja może przyjmować jakąś wartość ... ale nie musi ... może być asymptota pionowa,
jedno− lub dwustronna ... a może jej nie być ... jak chcesz
6 lut 11:22
mati: a miałbym jeszcze pytanie o asymptoty, tylko chwilka musiałbym je znaleźcć
6 lut 11:24
mati: f: R→R
limx→1− f(x)= 0
limx→1+ f(x)= +∞
limx→−∞ (f(x)+x)=0
limx→+∞ f(x)=0
I jakie asymptoty posiada funkcja :
pionową x=1 lewostronną
poziomą y=0 w −∞
ukośną y=−x w −∞
Czy takie ?
6 lut 11:28
wredulus_pospolitus:
pionową ... prawostronna (bo granica jest +/−∞)
poziomową w +∞ (bo granica lim f(x) = 0 <−−− granica 'skończona')
ukośną w −∞ bo lim(f(x) + 1*x) = 0 <−−− granica 'skończona' <−−− wskazówka: spójrz jak oblicza
się granicę ukośną ... jak wylicza się 'b')
6 lut 11:30
mati: b= lim (f(x)−ax)
6 lut 11:33
wredulus_pospolitus:
a w tym konkretnym przypadku a = (−1)
więc w −
∞ masz asymptotę ukośną y = −x
6 lut 11:36
wredulus_pospolitus:
uwaga ... gdyby było, że limx−>−∞ (f(x) + x) = +∞ to NIE JESTEŚ W STANIE OKREŚLIĆ czy masz
tam asymptotę poziomą/ukośną ... a jedynie wiesz, że y=−x nie jest asymptotą
6 lut 11:37
mati: Czyli prawie dobrze
6 lut 11:38
wredulus_pospolitus:
a konkretniej y=−x + c nie jest asymptotą (gdzie c∊R)
6 lut 11:38
mati: Jeszcze nie jestem pewny, to zapytam:
| | (−1)n | |
Mam sprawdzić czy ciąg jest ograniczony: |
| |
| | n2 | |
Sprawdzam czy granice podciągów a
2n i a
2n+1 są równe ?
lim a
2n = 0
lim a
2n+1 = 0
Czyli ciąg jest ograniczony, tak ?
6 lut 11:46
wredulus_pospolitus:
tak ... ciąg zbieżny jest ciągiem ograniczonym
wskazówka do policzenia granicy tego ciągu −−− tw. o 3 ciągach
6 lut 11:54
mati: a nie można zrobić tego tak jak zrobilem ?
6 lut 13:06
wredulus:
Mozna ... tylko z tw.o 3 ciagach masz szybciej
6 lut 13:13