dfhd Kmicic: JAk wyzanczyc kąt :

	1
cos(		π)
	12

Ada: Przy liczbach zespolonych coś tam wychodzi (są liczby, dla których wychodzi). Można rozwijać w szereg Taylora, ale tu uzyskujesz tylko przybliżenie.

Janek191:

	π
cos		= cos 15o
	12

Mamy cos 30^o = cos (2*15^o) = 2 cos² 15^o − 1 ; niech t = cos 15^o więc

√3
	= 2 t2 − 1 / * 2
2

√3 = 4 t² − 2 4 t² = √3 + 2

	√3 + 2
t2 =
	4

	√ √3 + 2		√ 4 √3 + 8		√ ( √6 + √2)2
t =		=		=		=
	2		4		4

	√6 + √2
=
	4

	√6 + √2
cos 15o =
	4

=========================

Kmicic: dzieks

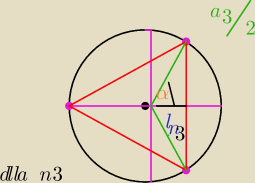5-latek: cosinus 15 stopni mozemy tez latwo obliczyc z zaleznosci geometrycznych Znajac dlugosc boku a_n wielokata foremnego wpisanego w kolo jednstkowe mozemy obliczc wartosc funkcji trygonometrycznych kata π/n . Jesli przyjmiemy za ramie poczatkowe kata promien dzielacy na polowy bok n−kata wpisanego w

	an2
kolo o promieniu R=1 to an/2 bedzie linia sinusa kata pi/n a apotema ln=√1−
	4

bedzie linia cosinusa W naszym przypadku wiemy ze n=12 to a₁2=√2−p[3} i l₁₂=U{√2+√3{2}

	pi		√3−1
Wobec tego sin		=sin15= U{√2−√3{2} =
	12		2√2

	pi		√3+1
natoniast cos		=U{√2+√3{2}=
	12		2√2

to tg15= 2−√3 Rysunek jest przykladowy dla trojkata rownobocznego