funkcja studentka M: Muszę wyznaczyć przedziały monotoniczności i ekstrema funkcji : x⁴ +4x³ +4x² 1.Wyznaczam dziedzine: Zb liczb rzeczywistych 2. Liczę pochodną i wyszła mi : 4x³ + 12x² +8x − dziedzina tego to również Zb liczb rzeczyw. 3. Wyliczyłam miejsca zerowe : 0 , −1 i −2 I właśnie teraz nie umiem narysować wykresu funkcji.. Pomoże ktoś? Skąd wiadomo czy funkcja biegnie nad osią x czy pod nią? Z góry bardzo dziękuje za pomoc i poświęcony czas

x3: Te "studentka" najpierw policz granicę x→+∞i x→−∞ i pamiętaj ,że twoja f(x) jest ciągła!

studentka M: Podręcznik z którego się uczę nic nie mówi o liczeniu granicy.. Z wykładów też nie mam takich notatek.. Liczyłam tak że funkcja jest rosnąca gdy pochodna jest większa od zera. Więc 4x(x+1)(x+2)>0 Ale jak to narysować?

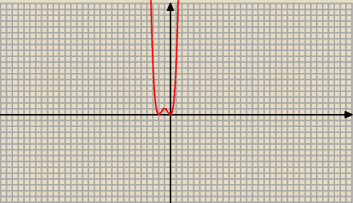
Janek191: Źle policzone miejsca zerowe !

Janek191: f(x) = x⁴ + 4 x³ + 4 x² = x²*( x² + 4 x + 4) = x²*( x + 2)² Miejsca zerowe: 0 i − 2

Janek191: Ja policzyłem miejsca zerowe danej funkcji , a nie pochodnej.

studentka M: aha.. Ale żeby określić monotoniczność to trzeba narysować wykres pochodnej, prawda?

studentka M: A mógłbyś mi wytłumaczyć jak się rysuje ten wykres? Bo na jego podstawie określam monotoniczność, ekstrema, wklęsłość i wypukłość..

grześ: Przy wielomianach stopnia 3ciego i wyższego, w zależności od tego jaki jest znak +/− przy najwyższej potędze to wykres zaczynać rysować od prawej strony od góry jeśli jest +, jeśli jest − to od dołu. I "odbijasz" lub "przechodzisz" za oś X w zależności czy pierwiastek powtarza się parzystą ilość razy czy nie.

wredulus_pospolitus: grześ ... w wielomianie 2 i 1 stopnia ta metoda także się sprawdza

grześ: Masz racje ale tam jest prościej kiedy współczynnik przy najwyższej potędze jest dodatni to ramiona idą w górę, ujemny to idą w dół. Ale to tyczy się tylko wielomianów stopnia 2giego.

Artur miast z mat to z telew: Miejsca zerowe policzone są podobno dobrze,a za to wykres funkcji narysowany żle Ale nie oto chodzi,Jak powiada docent K istotne jest,że: f '(x)=0 ⇔ x=tg150^o − 1 ⋁ x=tg30^o − 1 i teraz:

⎧	limf(x→−∞) =−∞
⎩	f[xek=tg150o −1]>−∞

Zatem f(x) rośnie x∊(tg150^o − 1;tg30^o −1) f(x) maleje

⎧	f[tg30o −1=xek]<∞
⎩	limf(x→∞)=∞

Zatem f(x) rośnie Funkcja jest ciągła

Obywatel: A najbardziej istotne jest to ,że te bandyckie telewizyjne ignoranckie pierdzistołki , nadal technicznie uprzywilejowane i nie można ich przycywilizować

Rycerz: Tralala

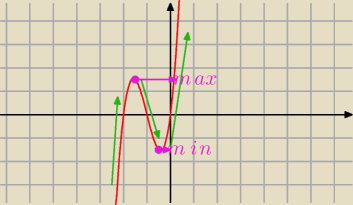
Aga1.: Oto wykres pochodnej

Aga1.: Na wykresie pochodnej nie zaznaczasz max i min , ani gdzie rosnąca ani malejąca. (zignoruj zielone strzałki i fioletowy zapis)

studentka M : Aga1 mogłabyś mi powiedzieć jak rysujesz ten wykres?

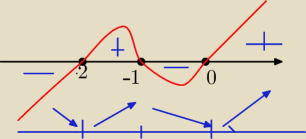
Aga1.: Zaznaczasz miejsca zerowe i rysujesz "węża" zaczynając od prawego górnego rogu, po dojściu do miejsca zerowego przechodzisz pod oś x, bo 0 jest pierwiastkiem jednokrotnym, Wracasz do środkowego miejsca zerowego i przechodzisz nad oś x i znów wracasz do miejsca zerowego i przechodzisz pod oś x. f_max=f(−1) f_min=f(−2)= f_min=f(0)=0 −podstawiasz do podanego wzoru.

studentka M : ok to rozumiem, a dlaczego od −1 do −2 biegnie nad osią x ? a od −2 znów pod osią?

Aga1.: Jeśli wszystkie pierwiastki są jednokrotne to znad osi x przechodzisz pod oś x, a spod osi x przechodzisz nad o x. (tak jakbyś biegła miedzy płotkami slalomem)

studentka M : aha już rozumiem, dziękuje Ci bardzo a jeszcze może być taka sytuacja że się "odbija" i kiedy sie to stosuje?

Aga1.: Odbijamy , gdy jest parzysta krotność pierwiastków np. y=(x−2)(x−5)⁴ x=2 − pierwiastek jednokrotny x=5 −pierwiastek 4−krotny (tu odbijasz)

studentka M : noo w końcu to zrozumiałam Aga1 jesteś Wielka! Naprawde dzieki