zadanko zawodus: Zadanie dla bezendu Wielomian na maturkę Dzieląc wielomian W(x) przez wielomian P(x)=x³−3x²−x−1 otrzymujemy trójmian Q(x)=x²+6x+19 oraz resztę 58x²+19x+22. Znajdź wielomian W(x) oraz rozwiąż nierówność W(x)≤2x³−7x.

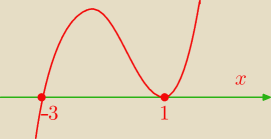
bezendu: W(x)=P(x)*Q(x)+R(x) W(x)=(x³−3x²−x−1)(x²+6x+19)+58x²+19x+22 W(x)=x⁵+3x⁴−6x²−6x+3≤2x³−7x W(x)=x⁵+3x⁴−2x³−6x²+x+3 W(x)=x⁴(x+3)−2x²(x+3)+(x+3) W(x)=(x+3)(x⁴−2x²+1) W(x)=(x+3)(x²−1)² (x+3)(x²−1)²≤0 x∊(−∞,−3<∪{1}

zawodus: To jest twoje ostateczne rozwiązanie?

bezendu: Tak.

zawodus: Jeśli miałbym ci oceniać jako egzaminator i za to zadanie byłoby za 4 punkty dostałbyś tylko 3

bezendu: Niby czemu ?

zawodus: Szukaj błędu

ZKS: bezendu a czy czasem x² − 1 się jeszcze nie rozkłada?

bezendu: Dzięki ZKS ! W(x)=(x+3)(x−1)²(x+1)² x∊(−∞,−3>∪{−1}∪{1}

ZKS: Teraz .

bezendu: To ja wracam do brył

zawodus: ok to następne zadanie Dany jest trapez prostokątny o podstawach a i b. Oblicz pole tego trapezu, jeśli wiadomo, że można wpisać w niego okrąg.

Mila: Właśnie miałam Ci Bezendu, przypomnieć, −−BRYŁKI.

jerey: trapeze prostokątny i da sie w niego wpisac okrąg to h=2r?

	a+b
P trapezu		*2r? gdzie r − promien okręgu
	2

bezi: Chyba coś zepsułem ale wyszlo mi ab

zawodus: Tak, tylko my mamy dane tylko podstawy.

zawodus: bezi pokaż swoje rozwiązanie wynik jest poprawny

bezi: h−wysokość c−drugie ramie c+h=a+b c=a+b−h Z twierdzenia pitagorasa (b−a)² + h²=(a+b−h)² b²−2ab+a² + h²=a²+2ab+b²−2ah−2bh+h² 4ab=2ah+2bh

2ab
	=h
a+b

I podstawilem do wzoru na pole trapezu.

zawodus: Bardzo ładnie