calka pole pom: oblicz pole obszaru y=6/x y=−x−5

wredulus_pospolitus: krok 1) rysujesz te funkcje krok 2) zaznaczysz punkty przecięcia krok 3) wyznaczasz algebraicznie punkty przecięcia krok 4) obliczasz calke oznaczoną koooniec

wredulus_pospolitus: natomiast polecam sprawdzić ponownie te dwie funkcje ... chyba coś się 'pierdyknąłeś' w pisaniu

pom: nie, dobrze przepisalam.

pom: wyjdzie calka od −3 do 2, z 6*lnx+1/2 x²+5x ?

pom: mam jeszcze jedno pytanie asymtota ukosna 1/2 x + arcctgx y=0

pom: czt to y=0?

wredulus_pospolitus: niee ... nie wyjdzie żadna cała od −3 do 2

6
	to hiperbola
x

−x−5 to prosta (malejąca)

	6
jedyny punkt wspólny to (−1,−1) ... innymi słowy f(x) = −x−5 to styczna do g(x)=		w
	x

x₀=−1

pom: y=1/2 x

wredulus_pospolitus: 12:29 bez liczenia (tak na czuja) obstawiałbym

	1
y =		x dla +/−∞
	2

Ajtek: 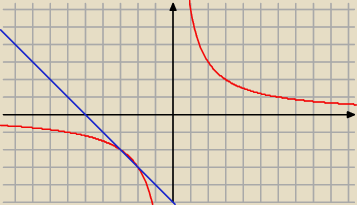wredulus rysunek mówi coś innego.

	6
Zresztą f(−1)=		=−6 a f(−1)−x−5=−4
	x

pom: przeciez jezeli przyrownamy do siebie te wielkosci i obliczymy delte to wydzie x=−3 lub x=−2

pom: dzieki

pom: a moglby ktos mniej wiecej narysowac ten wykres y = x/2 + arcctgx ? punkt przegiecia wyszedl mi 0 , a punkty stacjonarne to −1 to maximum ,a 1 to minimum