Wrzucam zadania z rozwiazaniami :) akante: 1.a xfy₁ ⋀ xfy₂ ⇒ y₁ = y₂ Nie moze tak byc bo mozna chyba miec dwie zony? 1.b xfy₁ ⋀ xfy₂ ⇒ |y₁| = |y₂| jest funkcją totalną x² = |y| wartosc bezwzgledna jest zawsze dodatnia kwadrat tak samo wiec jest totalna srednio juz pamietam jak to robic ale chyba jakos tak

PW: Wsisko totalnie loziumieć. Dwie ziony.

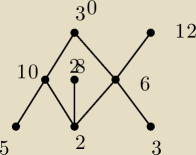
akante: 2,3,5,6,10,12,28,30 najwieksze:brak najmniejsze:brak minimalne:5,2,3 maksymalne :28,30,12 inf(2,4): jakim chujem jak tu nie ma czworki? sup(5,6,10): 30

Ajtek: Wartość bezwzględna jest zawsze dodatnia Kwadrat liczby jest zawsze dodatni

Ajtek: akante chyba nie ten wątek .

akante: jak macie jakies wskazowki to walcie wrzucam kolegom zadanka nie chce ich wprowadzac w blad a dawno nie robilem tych zadanek Ajtek jak inaczej udowodnic? X−Y ∊R a x²=|y|

Ajtek: Nie mam pojęcia . Ale 0²=0 nie jest dodatnie, |0|=0 również nie jest dodatnie.

akante: Wyznacz zbiory A,B,A∩B,A/B jeżeli A={x∊R:−x² +2x + 3≤0} B={x∊R:3x+1>−5}

akante: mhmm no tak masz racje ale w dalszym ciagu sie rowna co do wartosci a o to chodzi chyba przy sprawdzaniu czy jest totalna chociaz nie za bardzo pamietam

Ajtek: akante to zadanie ze zbiorami to śmiech przecież jest.

akante: nom

akante: ale na funkcjach z tym pierwszym mam problem

akante: A √Δ =4 x₁ = ^{−b − √Δ}_2a x₂ = ^{−b + √Δ}_2a x₁ = 3 x₂=−1 A=(−∞,−1> U <3,+∞) B 3x+1>−5 3x>−6 x>−2 B=(−2,+∞)

akante: A∩B=(−2,−1> U <3,+∞) A/B = (−∞,−2>

akante: jb cos zle bylo to poprawiaz prosze

Ajtek: Okej jest.

akante: 2. Udowodnij ze dla dowolnych zbiorow A,B,C Mamy: a)(B∩C)∪A = (B∪A)∩(C∪A) b)(A∩B)'=A'∪B' Ktos pomoze z drugim tutaj?

akante: ja to widze tak a) (x∊B⋀x∊C)⋁x∊A mhmm a co dalej ? troche juz pozapominalem korzystam z rodzielnosci ∨ wzgledem ∧ i wychodzi mi prawa strona czyli : (B∪A)∩(C∪A) to bylby wystarczjaacy dowod?

akante: zad 3. Na plaszczyznie z prostokatnym ukladem wspolrzednym zaznacz punkty ktorych wspolzedne naleza do iloczynu kartezjanskiego AxB gdy A =<−2;2> B=<−1,1> U {3} z tym tez mam problem ktos potrafi?

akante: z 4 Podaj wszystkie elementy zbiory potegowego P(A) gdy A={a,b,1,0} rozw. P(A) = {{Φ},{a},{b},{1},{0},{a,b},{a,1},{a,0},{b,1},{b,0},{1,0},{a,b,1},{a,b ,0},{0,b,1},{0,1,a},{a,b,1,0}}

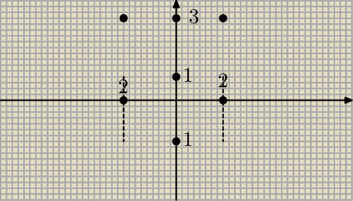
akante: tam jest minus jeden i dwa i to rozwiazanie trzeciego chyba nalezy do tego iloczynu to co zakratkowane i te dwie kropki na prawo i lewo od 3

akante: 9,0,1,2,4,7,6,3 wybieranie) 0,9,1,2,4,7,6,3 0,1,9,2,4,7,6,3 0,1,2,9,4,7,6,3 0,1,2,3,4,7,6,9 0,1,2,3,4,6,7,9 babelkowe) 0,9,1,2,4,7,6,3 0,1,9,2,4,7,6,3 0,1,2,9,4,7,6,3 0,1,2,4,9,7,6,3 0,1,2,4,7,9,6,3 0,1,2,4,7,6,9,3 0,1,2,4,6,7,9,3 0,1,2,4,6,7,3,9 0,1,2,4,6,3,7,9 0,1,2,4,3,6,7,9 0,1,2,3,4,6,7,9