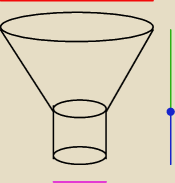
 oblicz objętość bryły
czarwone 6r
zielone i niebieskie − h
różowe 2r
oblicz objętość bryły
czarwone 6r
zielone i niebieskie − h
różowe 2r
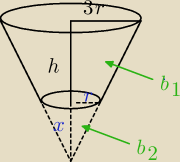 górna część bryły, to ścięty stożek, w którym:
górna część bryły, to ścięty stożek, w którym:
| x | x+h | ||
= | |||
| r | 3r |
| 1 | ||
x = | h | |
| 2 |
| 1 | 1 | |||
Vb1 = | π(3r)2(h+x) − | πr2x | ||
| 3 | 3 |
| 3 | 1 | 1 | ||||
Vb1 = 3πr2* | h − | πr2* | h | |||
| 2 | 3 | 2 |
| 9 | 1 | |||
Vb1 = | πr2h − | πr2h | ||
| 2 | 6 |
| 26 | ||
Vb1 = | πr2h | |
| 6 |
| 13 | ||
Vb1 = | πr2h | |
| 3 |
