trygonometria Marcela: może ktoś sprawdzić. zrobiłam zad i nie wiem czy dobrze. oto zadanie. liczby ^a+1_a oraz ^a+2_a ( a≠0) są odpowiedmio sinusem i cosinusem tego samego koąta ostrego.Oblicz a. i tak − korzystałam najpierw z 1− trygonometrycznej −układ równanń − ostateeczne równanie a²+6a+5=0 i pierwiastki a1=−5 i a2=−2. Czy dobrze?

Saizou :

	a+1
sinx=
	a

	a+2
cosx=
	a

(a+1)²+(a+2)²=a² a²+2a+1+a²+4a+4=a² a²+6a+5=0 (a+5)(a+1)=0 a=−5 a=−1 zał a+2>0→a>−2 a+1>0→a>−1 a>0 zatem nie ma takiego kąta

Łucja: tak pomyliłam sie w pierwiastkach . A czy na pewno nie ma takiego kąta? bo w sumie to miałam tylko a wyliczyc.

Saizou : dla a=−5 a to jak najbardziej bo na rysunku powinna być wartość bezwzględna z tych liczb

	−5+1		4
sinx=		=
	−5		5

	−5+2		3
cosx=		=
	−5		5

dla a=−1 sprzeczność (bo dla x∊(0:90^o) jest to fałsz) sinx=0 cosx=1 przepraszam bardzo

ICSP: taki trójkąt nie istnieje. Bo dla dowolnego dodatniego a zachodzi : a + 1 > a zatem

	a+1		a
sinα =		>		= 1
	a		a

Sprzeczność. Czasem wystarczy pomyśleć.

Saizou : też mi się tak wydawało, ale kolega mnie w bład wprowadził

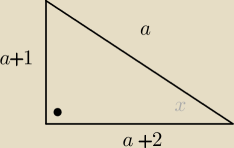
ICSP: Chociaż nie. Nigdzie nie jest powiedziane, że a+1 jest bokiem. Trójkąt 3,4,5 spełnia warunki zadania. Odp a = −5