.
bezendu:
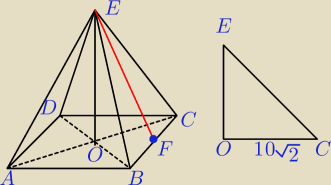
W ostrosłupie czworokątnym prawidłowym długość krawędzi podstawy jest równa 20, a miara kąta
| | 3√2 | |
nachylenia krawędzi bocznej do płaszczyzny podstawy jest równa α. Wiadomo, że tgα= |
| |
| | 2 | |
H=|OE|−wysokość ostrosłupa
h=|EF|−wysokość ściany bocznej
2H=60
H=30[j]
P
p=20
2=400[j
2]
H
2+(10
√2)
2=|EC|
2
|EC|
2=1100
|EC|=10
√11
|EF|
2=(10
√11)
2−(10)
2
|EF|
2=1000
|EF|=10
√10
P
b=400
√10[j
2]
P
c=400(1+
√10)[j
2]
Czy wszystko się zgadza, łącznie z zapisem ?
4 lut 16:02
bezendu:
Do tego samego zadania
B)Przez krawędzi podstaw tego ostrosłupa poprowadzono płaszczyznę prostopadłą do przeciwległej
ściany. Wyjaśnij jaką figurą jest przekrój ostrosłupa tą płaszczyzną.
Proszę o pomoc do tego podpunktu.
4 lut 16:16
Saizou :
tutaj jest błąd
|EF|
2=(10√11)
2−(10)
2
dlaczego 10
2
4 lut 16:16
Aga1.: Nie dostrzegłam błędu.
Można krócej , nie liczyć EC
h2=H2+102
4 lut 16:18
bezendu:
połowa krawędzi ?
4 lut 16:19
Saizou :
dokładnie tak
lEFl2+lCFl2=lECl2
lEFl2=lECl2−lCFl2 lCFl=5 lECl=10√11
4 lut 16:21
bezendu:
To mam coś nie tak ?
4 lut 16:22
Aga1.: ICFI=0,5IBCI=0,5*20=10
4 lut 16:24
bezendu:
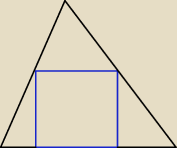
Ten przekrój tak będzie wyglądał ? Oczywiście równe odległości.
4 lut 16:27
Saizou : sorry jakoś sobie ubzdurałem że bok to 10
4 lut 16:30
Saizou :
4 lut 16:35
bezendu:
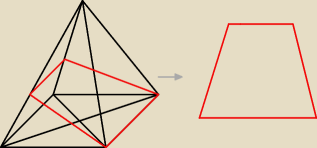
Czemu trapez ?
4 lut 16:36
Saizou : żeby to był kwadrat to musiałby lecieć po podstawie (co jest niemożliwe, bo ma być prostopadły
pod przeciwległej ściany), czyli to tak jakbyśmy podnosili podstawę do momentu kiedy będzie
ona prostopadła do ściany, a to co wychodzi za ostrosłup obcinamy, zatem powstałby trapez
4 lut 16:42
bezendu: Ale czemu nie tniemy od wierzchołka ?
4 lut 16:57
zawodus: Po prostu rysujesz wysokości dwóch ścian bocznych i łączysz i wyjdzie trapez...
4 lut 17:00
Saizou :
w sumie istnieje taka opcja żeby ciąć do wierzchołka, ale nie przy takich danych
a nie tniemy do wierzchołka , bo oś symetrii przekroju musi być prostopadła do przeciwległej
ściany
4 lut 17:01
bezendu: Dzięki przemyślę to
4 lut 17:19
bezendu: Już rozumiem czemu tak !.
4 lut 17:42
Saizou : to świetnie xd
4 lut 17:43
bezendu:
A czy zapis jest ok ? Bo ostatnio zostawiał wiele do życzenia..
4 lut 17:44
Saizou : jak dla mnie wystarczający
4 lut 17:47
bezendu: A dla innych ?
4 lut 22:49
4 lut 22:58
bezendu: Już zrobiłem
4 lut 23:13