m
Radek:
W(x)=x3+3x+1 względem symetrii x=2
czyli mam brać jakieś punkty W(x) i odbić względem x=2
3 lut 21:45
Mila:
Co to znaczy względem symetrii, podaj dokładnie polecenie.
3 lut 21:50
Radek:
Wykres W(x) przekształcono w symetrii względem prostej x=2
Pani wczoraj pokazywała mi przykłada ale tam było miejsce zerowe. A tutaj muszę szukać punktów
?
3 lut 21:52
zawodus: Robisz tak jak z punktem... tylko tutaj masz ich nieskończenie wiele...
3 lut 21:57
Radek:

Czy to jest ok ? Wiem, że muszę stworzyć układ z 3 nie wiadomymi więc wystarczą 3 punkty ?
3 lut 22:00
Mila:
Radek, masz podać wzór funkcji po tym przekształceniu?
3 lut 22:02
Radek: Tak.
3 lut 22:03
Eta:
wstaw za x do wielomianu i ..... na końcu opuść primy
3 lut 22:06
Radek:
A moje częściowe rozwiązanie nie jest poprawne ?
3 lut 22:10
Mila:
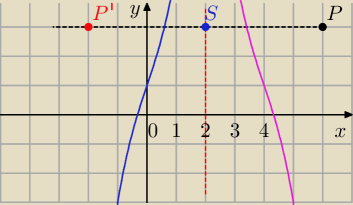
P(x,y) dany (dowolny) punkt
P'(x',y') punkt, który otrzymasz po przekształceniu puntu P przez symetrię względem prostej x=2
Zauważ, że S jest środkiem odcinka PP'
y'=y
S=(2,y)
x+x'=4
x'=x−4
x=4−x'
P'(x',y)=(4−x,y) druga współrzędna nie zmienia się.
podstawiamy do wzoru za x wyrażenie:(4−x')
w(x')=(4−x')
3+3(4−x')+1
w(x')=64−3*16x'+3*4x'
2−x'
3+12−3x'+1 mozemy opuścic znaczkl '
w(x)=−x
3+12x
2−51x+77 wzór po przekształceniu wykresu danego wielomianu
3 lut 22:26
Eta:

3 lut 22:30
Radek:
A czy moim sposobem też można by było zrobić to zadanie ? post 22:00 To teraz proszę o jakiś
przykład do samodzielnego zrobienia ?
3 lut 22:31
Mila:
dla 4 punktów i układ 4 równan z 4 niewiadomymi
w'(x)=ax3+bx2+cx+d
3 lut 22:36
Radek:
Dziękuję, a mogę prosić o przykład do rozwiązania ?
3 lut 22:39
Mila:
Radek podałyśmy Ci sposób zgodny ze sztuką. Nie jest to trudne,
a przyda Ci się w przyszłości, postaraj sie zrozumieć.
3 lut 22:40
Radek:
Ja rozumiem to przekształcenie

3 lut 22:42
Mila:
Wykres funkcji f(x)=x2+2x−1przekształcono przez symetrię względem względem prostej x=3.
Napisz równanie opisujące otrzymany wykres.
3 lut 22:48
Radek:
Ale jeszcze mam pytanie. Ma Pani ten punkt P'(x',y') i wyznaczyła Pani x' a podstawia Pani x ?
3 lut 22:55
Mila:
Zgadza się. We wzorze funkcji masz punkt x i za niego podstawiasz.
3 lut 22:58
Radek:
y=y'
S=(3,y)
x+x'=6
x=6−x'
y=(6−x')2+2(6−x')−1
y=x2'−12x'+36'+12−2x'−1
y=x2−14x+47
3 lut 23:04
Eta:

3 lut 23:05
Radek: Dziękuję

Jeszcze wstawię trochę zadań.
3 lut 23:08
Mila:
No, ładnie.
3 lut 23:12
Radek:
W wyniku jakiego przekształcenia (lub przekształceń) wykresu funkcji f (x) = x4+3x można
otrzymać wykres funkcji g , jeżeli
a) g(x) = (x − 5)4+3 (x−5)−5 ; przesunięcie o wektor v[5,−5]
b) g(x) = |x4+3x +1| ; przesunięcie o wektor [0,1] i −f(x) ?
3 lut 23:15
Radek: ?
3 lut 23:24
Mila:
b)f(x)→ T[0,1]→SOX dla y<0
3 lut 23:37
Radek: Sox dla y<0 skąd Pani ma taki zapis ?
3 lut 23:40
Mila:
Taki zapis oznacza, że odbijasz tylko tę część wykresu, która znajduje się pod osią OX.
Nie wiem skąd mam. Jak znajdę, to napiszę.
3 lut 23:56
Radek: i zawsze jest y>0 w takim zapisie ?
c) g(x) = x4+3|x|
3 lut 23:57
Aga1.: y≥0
c)
g(x)=f(IxI)
1)g(x)=f(x) dla x≥0
2)g(x)=f(−x) dla x<0
4 lut 08:13
Radek:
A można prosić o wytłumaczenie tego ostatniego przekształcenia ?
4 lut 13:59
zawodus: tzn?
4 lut 14:27
Mila:

Zostało odbite to co pod osią, czyli wszystkie punkty wykresu (x,y) gdzie y<0
4 lut 14:50
Radek: Chodzi o zapis tego ostatniego przekształcenia.
4 lut 14:51
Mila:
Czytaj 23:56.
4 lut 15:03
Radek:
A post Pani Agnieszki ?
4 lut 15:04
Mila:
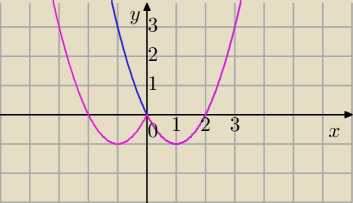
Przykład.
f(x)=x2−2x
"Odbijasz" względem osi OY tę część wykresu z prawej strony, część z lewej pomijasz ,
otrzymujesz wykres funkcji:
g(x)=x2−2|x|
4 lut 15:18
Radek:
Czyli takie odbicie to f(|x|) tak ?
4 lut 15:23
Mila:

Tak.
f(x)=x4+3x
g(x) = x4+3|x|
4 lut 15:27
Radek:
Dziękuję.
4 lut 15:28
Radek: A wytłumaczy mi Pani jeszcze kilka równań z wartością bez ?
4 lut 15:36
Mila:
Oczywiście.
4 lut 15:39
Radek:
Chodzi o takie równania jak mam np:
|x2−4|+|x+3|=3 ?
4 lut 15:41
Mila:
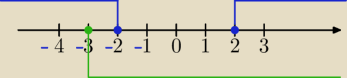
Najpierw przedziały:
|x
2−4|=x
2−4 dla x≤−2 lub x≥2
|x+3|=x+3 dla x≥−3
zaznaczam na osi, gdzie (x
2−4) i (x+3 ) są dodatnie
Teraz widzisz że możesz rozważyć w przedziałach:
(−
∞,−3)
<−3,−2>
(−2,2)
<2,
∞)
Ustalaj wzory i rozwiązuj.
4 lut 15:50
Radek:
1
0 x
2−4+(−x−3)=3
x
2−4−x−3−3=0
x
2−x−10=0
Δ=41
√Δ=
√41
2
0 x
2−4+x+3=3
x
2+x−4=0
Δ=17
√Δ=
√17
3
0 x
2−4+x+3=3
x
2+x−4=0
√Δ=17
4
0 x
2−4+x=3=3
x
2+x−4=0
4 lut 16:13
Mila:
Punkt 3o popraw .
4 lut 16:21
Radek:
3
0 (−2,2)
x
2−4+x+3=3
x
2+x−4=0
Δ=17
√Δ=
√17
4 lut 16:25
Radek: teraz ok ?
4 lut 17:54
zawodus: Wyrażenie x2−4 w przedziale (−2,2) jest ujemne, źle...
4 lut 18:04
Mila: Poprawiaj.
4 lut 18:24
zawodus: Chyba uciekł

4 lut 18:26
Radek:
−x2+4+x+3=3
−x2+x+4=0
x2−x−4=0
Δ=17
wychodzi to samo.
4 lut 18:31
Radek: Nigdzie nie uciekłem..
4 lut 18:32
zawodus: Nie wychodzi to samo

4 lut 18:33
Mila:

teraz dobrze.
4 lut 18:33
Radek:
A w tym wypadku |x2−4|+|x−2|=3
chodzi tylko jak zapisywać przedziały
4 lut 18:35
Radek: ?
4 lut 19:32
Mila:
Radek , podobnie, a nawet łatwiej , weź wzór z tamtego i napisz ,
na pewno potrafisz. Ja sprawdzę.
4 lut 20:15
Radek:

Ale chodzi, że tutaj się będą pokrywać ?
Ten jeden się pokrywa ?
4 lut 20:18
Mila:

To dobrze, masz tylko 3 przedziały, żebys wiedział jak zmieniać znaki, to tak zaznacz.
4 lut 20:42
Radek:
(−∞,−2>
<2,3)
<3,∞)
4 lut 20:48
Radek: ?
4 lut 21:10
Mila:
gdzie tam widzisz 3.
(−∞−2> U(−2,2)U<2,∞)
4 lut 21:23
Radek:
Nie na ten spojrzałem wykres. Czyli Dalej nie wiem.
4 lut 21:24
Mila:
No czego nie wiesz?
4 lut 21:34
Radek: Jak zapisać te przedziały..
Mam takie wrażenie, że nie zdążę przerobić wszystkiego tego czego nie umiem do matury.
4 lut 21:35
Mila:
|x2−4|+|x−2|=3
|x2−4|=x2−4 dla x2−4≥0 czyli dla x≤−2 lub x≥2
|x−2|=x−2 dla x≥2
Na osi zaznaczam, gdzie (x2−4) ma wartości dodatnie oraz x−2 ma wartości dodatnie.
masz na osi przedziały, 20:42
1)(−∞,−2>
x2−4+(−x+2)=3 i rozwiązujesz
2) (−2,2)
−x2+4+(−x+2)=3 i rozwiązujesz
3) <2,∞)
x2−4+x−2=3 i rozwiązujesz
4 lut 21:48
Radek: To mogę prosić o jakiś przykład tylko do ustalenia przedziałów ?
4 lut 21:50
Mila:
|x2−9|+|x+4|=6
4 lut 21:54
Mila:
|x2−9|+|x−4|=6
4 lut 21:54
Radek:

|x
2−9|+|x+4|=6
(−
∞,−3)
<−3,−2>
(−2,−2)
<−2,
∞)
?
4 lut 21:59
Mila:
Całkiem bez sensu.
4 lut 22:10
Marcin: A nie czasem
(−∞;−4)
<−4;−3>
<−3;3>
(3;+∞)?
4 lut 22:12
Radek: 10 (−∞,−4>
20 (−4,−3)
30 <−3,3)
40 <3,∞)
teraz ok ?
4 lut 22:13
Marcin: Pewnie że ok Radku

4 lut 22:15
Marcin: Wątpię że trafimy na maturze na równanie z aż czterema przedziałami

4 lut 22:16
Radek:
Ja wolę to umieć.
4 lut 22:16
Marcin: Jasne, jasne

Ja u siebie w rozwiązaniu źle przedziały podomykałem

4 lut 22:17
Radek:
|x2−9|+|x−4|=6
10 (−∞,−3)
20 <−3,3)
30 <3,4)
40 <4,∞)
4 lut 22:19
Mila:
Moze być.
4 lut 22:27
Radek: A czemu w tym przykładzie Pani napisała
|x2−4|+|x−2|=3
(−∞−2> U(−2,2)U<2,∞)
a może być tak
(−∞−2)
<−2,2)
<2,∞)
czy nie ?
4 lut 22:29
Mila:
Ja domykam tam, gdzie wyrażenie |..| jest ≥0.
x2−4=0 dla x=2 lub x=−2
ale wyrażenie −x2+4=0 też dla x=2 lub x=−2
tam funkcje mają wartość 0, a zmiana znaku jest dla x∊(−2,2)
4 lut 22:35
Radek: A mój sposób by przeszedł ?
4 lut 22:39
Mila:
Myślę,że tak.
4 lut 22:40
Radek: Dziękuję. Będzie Pani jeszcze na forum dziś ?
4 lut 22:42
Marcin: Przecież przedziały możemy zamykać tak jak chcemy. Czy się mylę?

4 lut 22:43
4 lut 22:58
 Czy to jest ok ? Wiem, że muszę stworzyć układ z 3 nie wiadomymi więc wystarczą 3 punkty ?
Czy to jest ok ? Wiem, że muszę stworzyć układ z 3 nie wiadomymi więc wystarczą 3 punkty ?
 P(x,y) dany (dowolny) punkt
P'(x',y') punkt, który otrzymasz po przekształceniu puntu P przez symetrię względem prostej x=2
Zauważ, że S jest środkiem odcinka PP'
y'=y
S=(2,y)
P(x,y) dany (dowolny) punkt
P'(x',y') punkt, który otrzymasz po przekształceniu puntu P przez symetrię względem prostej x=2
Zauważ, że S jest środkiem odcinka PP'
y'=y
S=(2,y)



 Jeszcze wstawię trochę zadań.
Jeszcze wstawię trochę zadań.
 Zostało odbite to co pod osią, czyli wszystkie punkty wykresu (x,y) gdzie y<0
Zostało odbite to co pod osią, czyli wszystkie punkty wykresu (x,y) gdzie y<0
 Przykład.
f(x)=x2−2x
"Odbijasz" względem osi OY tę część wykresu z prawej strony, część z lewej pomijasz ,
otrzymujesz wykres funkcji:
g(x)=x2−2|x|
Przykład.
f(x)=x2−2x
"Odbijasz" względem osi OY tę część wykresu z prawej strony, część z lewej pomijasz ,
otrzymujesz wykres funkcji:
g(x)=x2−2|x|
 Tak.
f(x)=x4+3x
g(x) = x4+3|x|
Tak.
f(x)=x4+3x
g(x) = x4+3|x|
 Najpierw przedziały:
|x2−4|=x2−4 dla x≤−2 lub x≥2
|x+3|=x+3 dla x≥−3
zaznaczam na osi, gdzie (x2−4) i (x+3 ) są dodatnie
Teraz widzisz że możesz rozważyć w przedziałach:
(−∞,−3)
<−3,−2>
(−2,2)
<2,∞)
Ustalaj wzory i rozwiązuj.
Najpierw przedziały:
|x2−4|=x2−4 dla x≤−2 lub x≥2
|x+3|=x+3 dla x≥−3
zaznaczam na osi, gdzie (x2−4) i (x+3 ) są dodatnie
Teraz widzisz że możesz rozważyć w przedziałach:
(−∞,−3)
<−3,−2>
(−2,2)
<2,∞)
Ustalaj wzory i rozwiązuj.


 teraz dobrze.
teraz dobrze.
 Ale chodzi, że tutaj się będą pokrywać ?
Ten jeden się pokrywa ?
Ale chodzi, że tutaj się będą pokrywać ?
Ten jeden się pokrywa ?
 To dobrze, masz tylko 3 przedziały, żebys wiedział jak zmieniać znaki, to tak zaznacz.
To dobrze, masz tylko 3 przedziały, żebys wiedział jak zmieniać znaki, to tak zaznacz.
 |x2−9|+|x+4|=6
(−∞,−3)
<−3,−2>
(−2,−2)
<−2,∞)
?
|x2−9|+|x+4|=6
(−∞,−3)
<−3,−2>
(−2,−2)
<−2,∞)
?


 Ja u siebie w rozwiązaniu źle przedziały podomykałem
Ja u siebie w rozwiązaniu źle przedziały podomykałem 
