stycznej równanie Anja: Wyznacz równanie stycznej do okręgu o równaniu x²−8x+y²+2y=8 prostopadłych do prostej

	1
y=		x−7
	2

pomocy, analityczna to dla mnie czarna magia

zawodus: to trzeba iść do czarnoksiężnika...

Anja: ok, moze obedzie się bez czarnoksiężnika.... środek i promien jakos znalazłam

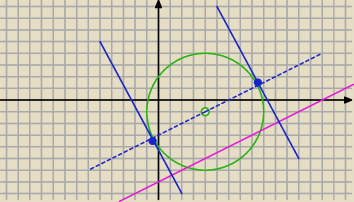
Bizon: x²−8x+16−16+y²+2y+1−1=8 (x−4)²+(y+1)²=25 Napisz równanie prostej równoległej do danej prostej i przechodzącej przez środek okręgu

Bizon: Potem poszukaj punktów przecięcia się tej prostej z okręgiem a potem to już wiesz co ... −

Bizon: Można oczywiście inaczej. Równanie kierunkowe stycznych y=−2x+b przyrównaj do równania okręgu i Δ=0

Anja: właśnie 2 sposób prostszy

Anja: Bizon, ale skąd tu wziąć delte? bo wyszła mi wartość bezwzględna czyli dwie opcje b...

Eta: 3 sposób S(4,−1), r= 5 styczna ma równanie : y= −2x+b ⇒ 2x+y−b=0 Odległość d środka S od stycznej jest d=r=5

	|4*2−1*1−b|
d=		=5 ⇒ |7−b|= 5√5 teraz dokończ
	√4+1

b=.... v b=.....