monotoniczność funkcji
Sadman: na podstawie def. zbadać monotoniczność funkcji:
f(x) = −2x + 3
x1<x2
x1−x2<0
f(x1)−f(x2) <0
czyli:
−2x1+3 − (−2x2+3) < 0
−2x1+3 + 2x2 − 3 < 0
tak?
3 lut 14:15
wredulus_pospolitus:
no ... niby tak ... ale to co napisałeś jest definicją funkcji rosnącej
a tutaj na pierwszy rzut oka widać, że ta prosta maleje

3 lut 14:17
Sadman: bo tak szczerze, to nigdy nie wiem od czego wychodzić. Czyli z tego co napisałam powinnam
wywnioskować, że funkcja nie jest rosnąca?

Nie cierpie tego tematu
3 lut 14:19
wredulus_pospolitus:

no tak w końcu:
−2x
1+3 + 2x
2 − 3 < 0
−2x
1 + 2x
2 < 0
x
1 − x
2 > 0
x
1 > x
2 
3 lut 14:20
Sadman: ...ale ciemnota

dzięki znowu
3 lut 14:22
Sadman: a co gdy mam (x−1)2 ?
doszłam do: x1(x1 −2) − x2(x+2x2) < 0
3 lut 14:30
Sadman: aa, ok to rosnąca
3 lut 14:32
wredulus_pospolitus:
Sadman −−− posluchaj ... zadania z analizy które w treści mają' wykaż, że' 'udowodnij' ,
'zbadaj' zaczynasz rozwiązywać (tak jak treść nakazuje) dopiero wtedy gdy już masz narysowaną
daną funkcję, ciąg czy co tam masz.
zauważ, że f(x) = (x−1)
2 to jest PARABOLA

a skoro masz parabolę ... to funkcja NIE JEST monotoniczna (jest najpierw malejąca a później
rosnąca) ... więc szybko wskazujesz x
0 = 1
i teraz wykazujesz, że:
x
1 < x
0
f(x
1) > f(x
0) (malejąca)
a dla x
2> x
0
f(x
2) > f(x
0) (rosnąca)
a więc w całości jest ona ? Nie monotoniczna

3 lut 14:34
wredulus_pospolitus:
niemonotoniczna*
3 lut 14:34
Sadman: jeju, chyba sobie daruje te monotoniczności
3 lut 14:35
wredulus_pospolitus:
możesz też to wykazać w ten sposób:
1) zakładam, że jest rosnąca:
kontrprzykład:
x1 = −9 ; x2 = 0
czyli nie jest rosnąca
2) zakladam, że jest malejąca:
kontrprzykład:
x1 = 0 ; x2 = 9
czyli nie jest malejąca
czyli funkcja nie jest ani malejąca ani rosnąca (w całej swojej dziedzinie) więc nie jest ona
monotoniczna (w całej swojej dziedzinie).
3 lut 14:36
Sadman: to chyba wykracza poza zakres moich możliwości

3 lut 14:36
wredulus_pospolitus:
Sadman ... analiza jest fajna

tu się tak kombinuje ... robi zadania nic nie wiedząc

wystarczy sobie narysować

3 lut 14:42
Sadman: bardzo fajna :c darzę ją ogromnym negatywnym uczuciem

jeszcze jak są łatwe przykłady, to ujdzie (tak, tak, mi nawet przy łatwych nie wychodzi

),
ale co dopiero gdy do akcji wkraczają eeee, logarytmy i inne sinusykotangensy
3 lut 14:45
Sadman: a na egzaminie to i tak pewnie dadzą w turobkosmos trudności
3 lut 14:46
wredulus_pospolitus:
tia ... na pewno dadzą turbokosmos ... a się zdziwisz jak zobaczysz te (proste) zadania
czasy gdy z uczelni wywalano 80% rocznika już dawno minęły ... teraz wykładowcy musza się
napocić aby wywalić JEDYNIE 20%

3 lut 14:51
Sadman: o wywalenie to ja się nie martwię

Bardziej o mój nagły zanik matematycznych umiejętności

mogę Cię jeszcze wykorzystać? Mam zbadać różnowartościowość funkcji a w przypadku gdy funkcja
nie jest różnowartościowa, to wyznaczyć te przedziały gdzie jest, no i mam:
| | x | | 1 | |
i zrobiłam, że |
| = |
| |
| | x1 | | x2 | |
i to koniec?

dla mnie jest różnowartościowa... ;c
3 lut 14:56
wredulus_pospolitus:
Sadman ... jeszcze raz ... narysuj zanim zaczniesz rozwiązywać

3 lut 15:01
wredulus_pospolitus:
z rysunku od razu widać, ze to funkcja różnowartościowa
a więc już wiesz co masz wykazać

więc to wykazujemy
∀
x1,x2∊Df x
1≠x
2 => f(x
1) ≠ f(x
2)
niewprost
niech x
1≠x
2 ⋀ f(x
1) = f(x
2) (czyli f(x
1)−f(x
2)=0)
| 1 | | 1 | | x2−x1 | |
| − |
| = |
| = 0 ⇔ x2−x1 = 0 ⇔ x1 = x2 |
| x1 | | x2 | | x1*x2 | |
sprzeczne
c.n.w.
3 lut 15:06
Sadman:
kurczę, a mi się tak nie chcę :c trzeba zawsze rysować?

o coś takiego mi wyszło mniej więcej
3 lut 15:09
Sadman: a ok

3 lut 15:10
Sadman: jak nic chyba sobie odpuszczę to

3 lut 15:11
wredulus_pospolitus:
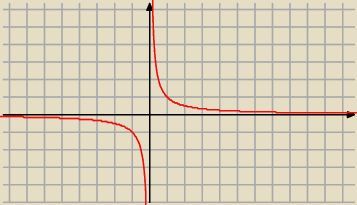
3 lut 15:14
Sadman: no, to mi też tak wyszło

trochę mniej wyględnie, ale jednak
3 lut 15:18
Sadman: hm, a jak to jest z tą okresowością? Mam sprawdzić czy podane funkcje są okresowe, i jeżeli tak
to wyznaczyć ten okres podstawowy, np.
f(x) = −sin(5x)
podstawiam:
−sin(5x) = −sin(5x+t)
i co dalej?

3 lut 15:42
Sadman: upup
3 lut 15:48
asdf: wredulus, 80% nie, ale 50% to na mojej uczelni standard

3 lut 15:58
Sadman: 
to ciekawe jak u mnie, ale wydaje mi się, że mniej

3 lut 15:59
wredulus_pospolitus:
asdf ... bo Ty to masz bogatą uczelnię

mało która uczelnia (wydział ... kierunek) sobie na to pozwoli ... bo za studentów dostają
'kasę' ... a kasę dostają za studenta co dotrwa do 2 roku

3 lut 15:59
wredulus_pospolitus:
no chyba że jest to jakiś oblegany kierunek jak np. budownictwo lądowe ... gdzie na 2 roku
zaczynają się laboratoria więc trzeba zrobić odsiew i z 500 zostawić te 200

bo się wydział
nie wyrobi z zajęciami w laboratoriach

3 lut 16:00
Sadman: ok ok

a co z tą okresowością?

3 lut 16:02
wredulus_pospolitus:
Sadman ... i tutaj ... zanim zaczniesz robić ... rysujesz

sinx jaki ma okres (hmmm ciekawe

)
a −sinx będzie miał w takim razie taki sam okres
no to sin(5x) będzie miał dłuższy okres a może krótszy

jak uważasz

3 lut 16:04
Sadman: ale na pewno się też da zrobić bez rysunku

sinx ma normalnie 2pi,
dłuższy? c:
3 lut 16:05
wredulus_pospolitus:
krótszy

a dlaczego

już tłumaczę:
3 lut 16:06
Sadman: no przecież zgadywałam

3 lut 16:07
wredulus_pospolitus:
sinx ma okres długości 2π ponieważ sinx = sin(x+2π)
| | 2π | | 2π | |
sin(5x) będzie miał okres .... |
| ... ponieważ: sin(5(x+ |
| ) = sin(5x + 2π) = sin5x |
| | 5 | | 5 | |
3 lut 16:08
wredulus_pospolitus:
fajnie by bylo gdybyś potrafiła sobie narysować podstawowe funkcje trygonometryczne oraz np.
sin(2x) ... cos(2x) ... sin(x/2) ... utrwalić w główce i będzie oczywistą oczywistością

3 lut 16:09
Sadman: hm, a np. 3cos(x+pi/2)?
już mnie głowa boli
3 lut 16:15
Sadman: ps Tobie się tak chce pomagać? w które zadanie nie wejdę, tam zielono

3 lut 16:17
Sadman: to normalnie ostatni przykład i biorę się za te durne pochodne, całeczki i szeregi. Mózg to mi
chyba spuchł do rozmiarów arbuza

3 lut 16:22
zawodus: Zrób screena i wyślij

3 lut 16:25
Sadman: ale czego?

3 lut 16:25
zawodus: "to normalnie ostatni przykład i biorę się za te durne pochodne, całeczki i szeregi. Mózg to mi
chyba spuchł do rozmiarów arbuza"
3 lut 16:26
Sadman: chętnie bym zrobiła, ale chyba się nie zmieści w kadrze

3 lut 16:27
wredulus:
Ten ostatni przyklad −−− okres bedzie ten sam co zwyklego cosx ... bo to π/2 to tylko
przesuniecie wzdluz osi ox
3 lut 16:30
Sadman: straciłeś swoją zieloność.
Okej, dzięki wielkie za pomoc

myślę, że chyba czas na przerwę, bo od rana tłukę tylko te
funkcje i jeszcze chwila, a będę zdrapywać ten "mózg" ze ściany

3 lut 16:31
wredulus:
Stracilem bo przesedlem z kompa na komorke
3 lut 16:33
Sadman: żeby tak można było na egzaminie tutaj zajrzeć

3 lut 16:33
Ajtek:
Na egzaminie Tobie nikt stąd nie pomorze

.
3 lut 16:34
zawodus: pomorze

nie pomoże

3 lut 16:35
Piotr 10: Może
Ajtkowi chodziło o Pomorze Gdańskie

3 lut 16:36
Ajtek:
Cicho


3 lut 16:37
5-latek: Witaj
Ajtek 
Popraw blad bo sie zaraz rzuca na Ciebie
3 lut 16:38
Ajtek:
Spoko, spoko, dam radę. Cześć
5−latek.
Pośmiejmy się, śmiech to zdrowie

.
3 lut 16:39
Sadman: oj, wcale bym nie pisała, że jestem na egzaminie i czekam na pomoc

użyję swoich leniwych
szarych komórek :3
3 lut 16:39
Sadman: to dzięki jeszcze raz za pomoc

coś czuję, że jeszcze dzisiaj się tutaj odezwę.
Miłego Wam!
3 lut 16:40
Ajtek:
Tutaj egzamin wyczuwa się na odległość

3 lut 16:40
Sadman: A to okej

Zresztą nawet sobie nie wyobrażam, że miałabym używać tel. na egzaminie

chyba
bym padła z nerwów

3 lut 16:42
3 lut 16:58
Sadman: biedne kobitki

ja się jeszcze nie zaczęłam stresować, najgorszy moment jak się dostanie
egzamin do ręki, zobaczy się szybko zadania i nagle pustka w głowie

i to wszystko przez
jakieś liczbowe wygibasy, a później już leci spokojnie

chyba, że nadejdzie głód i ten
stresik, że zaraz pół sali usłyszy jak mój brzuch warczy i że ktoś to pomyli z rewolucjami po
fasolce

koniec przerwy, głowa trochę odpoczęła to wracam do tego pięknego przedmiotu, jakim jest
matematyka

3 lut 18:25

 Nie cierpie tego tematu
Nie cierpie tego tematu
 no tak w końcu:
−2x1+3 + 2x2 − 3 < 0
−2x1 + 2x2 < 0
x1 − x2 > 0
x1 > x2
no tak w końcu:
−2x1+3 + 2x2 − 3 < 0
−2x1 + 2x2 < 0
x1 − x2 > 0
x1 > x2 
 dzięki znowu
dzięki znowu
 a skoro masz parabolę ... to funkcja NIE JEST monotoniczna (jest najpierw malejąca a później
rosnąca) ... więc szybko wskazujesz x0 = 1
i teraz wykazujesz, że:
x1 < x0
f(x1) > f(x0) (malejąca)
a dla x2> x0
f(x2) > f(x0) (rosnąca)
a więc w całości jest ona ? Nie monotoniczna
a skoro masz parabolę ... to funkcja NIE JEST monotoniczna (jest najpierw malejąca a później
rosnąca) ... więc szybko wskazujesz x0 = 1
i teraz wykazujesz, że:
x1 < x0
f(x1) > f(x0) (malejąca)
a dla x2> x0
f(x2) > f(x0) (rosnąca)
a więc w całości jest ona ? Nie monotoniczna 

 tu się tak kombinuje ... robi zadania nic nie wiedząc
tu się tak kombinuje ... robi zadania nic nie wiedząc  wystarczy sobie narysować
wystarczy sobie narysować 
 jeszcze jak są łatwe przykłady, to ujdzie (tak, tak, mi nawet przy łatwych nie wychodzi
jeszcze jak są łatwe przykłady, to ujdzie (tak, tak, mi nawet przy łatwych nie wychodzi  ),
ale co dopiero gdy do akcji wkraczają eeee, logarytmy i inne sinusykotangensy
),
ale co dopiero gdy do akcji wkraczają eeee, logarytmy i inne sinusykotangensy

 Bardziej o mój nagły zanik matematycznych umiejętności
Bardziej o mój nagły zanik matematycznych umiejętności  mogę Cię jeszcze wykorzystać? Mam zbadać różnowartościowość funkcji a w przypadku gdy funkcja
nie jest różnowartościowa, to wyznaczyć te przedziały gdzie jest, no i mam:
mogę Cię jeszcze wykorzystać? Mam zbadać różnowartościowość funkcji a w przypadku gdy funkcja
nie jest różnowartościowa, to wyznaczyć te przedziały gdzie jest, no i mam:
 dla mnie jest różnowartościowa... ;c
dla mnie jest różnowartościowa... ;c

 więc to wykazujemy
∀x1,x2∊Df x1≠x2 => f(x1) ≠ f(x2)
niewprost
niech x1≠x2 ⋀ f(x1) = f(x2) (czyli f(x1)−f(x2)=0)
więc to wykazujemy
∀x1,x2∊Df x1≠x2 => f(x1) ≠ f(x2)
niewprost
niech x1≠x2 ⋀ f(x1) = f(x2) (czyli f(x1)−f(x2)=0)
 kurczę, a mi się tak nie chcę :c trzeba zawsze rysować?
kurczę, a mi się tak nie chcę :c trzeba zawsze rysować?  o coś takiego mi wyszło mniej więcej
o coś takiego mi wyszło mniej więcej



 trochę mniej wyględnie, ale jednak
trochę mniej wyględnie, ale jednak


 to ciekawe jak u mnie, ale wydaje mi się, że mniej
to ciekawe jak u mnie, ale wydaje mi się, że mniej 
 mało która uczelnia (wydział ... kierunek) sobie na to pozwoli ... bo za studentów dostają
'kasę' ... a kasę dostają za studenta co dotrwa do 2 roku
mało która uczelnia (wydział ... kierunek) sobie na to pozwoli ... bo za studentów dostają
'kasę' ... a kasę dostają za studenta co dotrwa do 2 roku 
 bo się wydział
nie wyrobi z zajęciami w laboratoriach
bo się wydział
nie wyrobi z zajęciami w laboratoriach 
 a co z tą okresowością?
a co z tą okresowością? 
 sinx jaki ma okres (hmmm ciekawe
sinx jaki ma okres (hmmm ciekawe  )
a −sinx będzie miał w takim razie taki sam okres
no to sin(5x) będzie miał dłuższy okres a może krótszy
)
a −sinx będzie miał w takim razie taki sam okres
no to sin(5x) będzie miał dłuższy okres a może krótszy  jak uważasz
jak uważasz 
 sinx ma normalnie 2pi,
dłuższy? c:
sinx ma normalnie 2pi,
dłuższy? c:
 a dlaczego
a dlaczego  już tłumaczę:
już tłumaczę:







 myślę, że chyba czas na przerwę, bo od rana tłukę tylko te
funkcje i jeszcze chwila, a będę zdrapywać ten "mózg" ze ściany
myślę, że chyba czas na przerwę, bo od rana tłukę tylko te
funkcje i jeszcze chwila, a będę zdrapywać ten "mózg" ze ściany 

 .
.
 nie pomoże
nie pomoże 



 Popraw blad bo sie zaraz rzuca na Ciebie
Popraw blad bo sie zaraz rzuca na Ciebie
 .
.
 użyję swoich leniwych
szarych komórek :3
użyję swoich leniwych
szarych komórek :3
 coś czuję, że jeszcze dzisiaj się tutaj odezwę.
Miłego Wam!
coś czuję, że jeszcze dzisiaj się tutaj odezwę.
Miłego Wam!

 Zresztą nawet sobie nie wyobrażam, że miałabym używać tel. na egzaminie
Zresztą nawet sobie nie wyobrażam, że miałabym używać tel. na egzaminie  chyba
bym padła z nerwów
chyba
bym padła z nerwów 


 jak ja uwielbiałem takie
jak Ty wkurzać swoim 'spokojem ducha'
jak ja uwielbiałem takie
jak Ty wkurzać swoim 'spokojem ducha' 
 ja się jeszcze nie zaczęłam stresować, najgorszy moment jak się dostanie
egzamin do ręki, zobaczy się szybko zadania i nagle pustka w głowie
ja się jeszcze nie zaczęłam stresować, najgorszy moment jak się dostanie
egzamin do ręki, zobaczy się szybko zadania i nagle pustka w głowie  i to wszystko przez
jakieś liczbowe wygibasy, a później już leci spokojnie
i to wszystko przez
jakieś liczbowe wygibasy, a później już leci spokojnie  chyba, że nadejdzie głód i ten
stresik, że zaraz pół sali usłyszy jak mój brzuch warczy i że ktoś to pomyli z rewolucjami po
fasolce
chyba, że nadejdzie głód i ten
stresik, że zaraz pół sali usłyszy jak mój brzuch warczy i że ktoś to pomyli z rewolucjami po
fasolce  koniec przerwy, głowa trochę odpoczęła to wracam do tego pięknego przedmiotu, jakim jest
matematyka
koniec przerwy, głowa trochę odpoczęła to wracam do tego pięknego przedmiotu, jakim jest
matematyka 