paramtery funkcje Anka : Kto pomoże załamanej maturzystce ? prosze , nie ogarniam zadania a matura za 3 miesiące, to straszne ! pomocy! dla jakich wartości parametru m funkcja (m−1)x+m dla x<1 f(x)={ x² +(m−2)x+4−2m dla x≥1 przyjmują tylko dodatnie wartości I tak. więc zadanie zaczełam tak, jeśli funcja ma przyjmować dodatnie wartości to (m−1)<0 bo to będzie wtedy funkncja malejąca. i nastepnie (m−1)x+m >0 ( bo wartości dodatnie przyjmuje ) i ta druga część funkcji też musi być większa od zera, I tyle z mojej strony, nie moge dalej ruszyć. dlatego prosze o wytłumaczenie w razie możliwości ,Dzieki z góry. Anka pozdrawiam ,

Marcin: O! widzę że powoli zaczynają się budzić tegoroczni maturzyści. Siema

Bizon: a czy Ty sama rozumiesz co piszesz? Zgaduj−zgadula to na innej stronce Zacznij od porządnego przepisania zadania

Anka : Chyba czas najwyższy, lepiej późno niz wcale, jednak wcale mi nie jest do śmiechu że to nie 2 ze nie rok ze nawet nie pół roku tylko 3 miesiące....

Anka : ta klamerka obejmuje te dwie części funkcji. Ta cała funkcja ma przyjmować tylko wartości dodatnie, więc nie rozumie, Bizonie, czemu sie oburzasz

Bizon: ... nie oburzam tylko szkoda czasu na domysły

Anka : oczywiście ,przynaję, że na innych stronach jest to zadanie rozwiązane lecz tylko rozwiazanie mnie nie zadowala. Porszę również o wytłumaczenie. Wiec jesli ktos mógłby mi pomoc, byłabym zadowolona.

Bizon: skąd jest to zadanko?

Anka : czy moge liczyc na pomoc ?

Bizon: tak

Bizon: .. to chytre zadanko ... "pachnie" mi zbiorem Kiełbasy 1^o Rozpatrujesz funkcję w pierwszym przedziale Warunek m−1<0 jest prawidłowy ... ale nie wystarczający musi dodatkowo zachodzić f(1)>0 Zatem: m−1<0 i m−1+m>0

	1
Część wspólna dla tego przedziału to m∊(		,1)
	2

Czy to jest zrozumiałe?

Anka: http://www.zadania.info/3639895 zadanier pochodzi z tej strony. Tak jst to wytłumaczone, jednak dlaej tego nie rozumiem. Na prawde byłabym wdzięczna za wytłumaczenie tego jeszccze raz w maire możliwości krok po kroku, szczegolowo.

Rafał28: Zobacz tutaj: http://www.zadania.info/9080793

PW: No skoro w grę wchodzi "Porszę", to jedziemy. (m−1)x+m > 0 dla x<1 Oznacza to, że a) dla m=1 mamy do czynienia z nierównością 1 >0 − prawdziwą w całej dziedzinie (−∞, −1) b) dla m≠1 mamy nierówność (m−1)x+m > 0, x∊(−∞, −1). Oznacza ona, że współczynnik kierunkowy prostej jest ujemny i przecina ona oś OX w punkcie x₀=−1. Warto to sobie narysować, wtedy stanie się jasne.

	−m
m−1 <0 i x0 =		= −1
	m−1

m < 1 i −m = −m+1 − Ooo, to jest niemożliwe, ostał się więc ino m=1, z którym udajemy się do "dolnego przepisu" na funkcję f.

Anka: Mam pytanie, f(1)>0 −−> ten pprzypadek jest dlatego że ta funkcja liniowa musi przyjmować wartości dodatnie. ?

Bizon: .. no tak ... jeśli przyjmie się, że 0 to wartość dodatnia Dla mnie 0 to wartość nieujemna

Bizon: PW namieszał bo nie zrozumiał zadania −

Anka: Właśnie, Bizon, Bo na tej stronce, na któej podałam przyjmują że zero to wartość dodatnia .I właśnie też się nad tym zastanawiałam, bo mnie uczono, że 0 jest nieujemne.. a co z drugą cześcią funkcji?

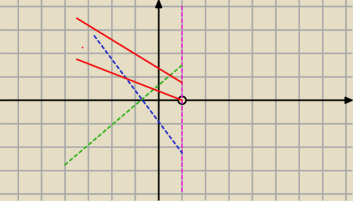
Bizon: ... może ten rysunek pomoże 1. oczywiście proste a dodatnim wsp. kierunkowym (jak to zielona) odpadają 2. ale odpadają też niektóre z ujemnym współczynnikiem (jak ta niebieska) 3. dopiero te czerwone dla których f(1)>0 spełniają drugi warunek

Bizon: do drugiej wrócimy jak zrozumiesz pierwszą −

PW: Nie, źle. Muszę się sam skrytykować uroczyście. Owszem, współczynnik kierunkowy m−1 < 0, ale żeby nierowność (m−1)x + m > 0 była spełniona dla wszystkich x∊(−∞,1) musi być (m−1)•1 + m ≥ 0 (radziłem narysować, a sam tego nie zrobiłem − funkcja liniowa o równaniu y = (m−1)x+m musi być na prawym krańcu − w jedynce − dodatnia lub równa zeru). Dlatego m−1 < 0 i 2m − 1 ≥ 0, czyli

	1
m∊[		, 1)
	2

Podsumowanie: "górny przepis" oznacza funkcję dodatnią na całej dziedzinie (−∞, 1) dla

	1		1
m∊[		, 1) ∪ {1} = [		, 1].
	2		2

PW: Bizon, zrozumiał, zrozumiał, tylko był zbyt pewny siebie (grzech nr 1).

Anka: Bizon, ten rysunek rzeczywiście ułatwił mi życie, dziękuję zrozumiałam, możemy przejść dalej

Bizon: drugą część można "załatwić" na kilka sposobów. Tam omówili sposób wierzchołkiem Ale znów "pomogę" Ci rysunkiem

Anka: ratujesz mi zycie !

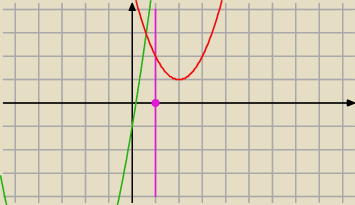
Bizon: Warunki spełnia i taka parabola i taka

Bizon: tam masz wyjaśniony sposób z wierzchołkiem

	b
xw=−
	2a

	−m+2
w warunkach naszego zadania xw=
	2

i opisane jest to chyba przystępnie

Bizon: podam Ci też inny sposób policzmy Δ Δ=m²+4m−12 Sprawdźmy gdzie jest ona większa a gdzie mniejsza od 0 Δ'=64 m₁=−6 m₂=2 ale nas interesuje przedział z pierwszego punktu zadania W przedziale tym Δ jest mniejsza od 0 ...współczynnik przy x² dodatni ... czyli parabolka nad osią. Czyli ta części zadania nie wnosi nowych ograniczeń Rozwiązaniem jest przedział z części pierwszej

Anka: hmm nie do konca rozumiem dlaczego trzeba liczyć wierzchołek tej paraboli i jaki to ma zwiaek z dalszymi obliczeniami

Bizon: Gdyby nie ograniczenia części pierwsze musiałabyś rozpatrywać oba nieudolnie narysowane przeze mnie przypadki. Ale skoro m ma spełniać obie funkcje to po prostu sprawdzasz z czym masz do czynienia −

Anka: ok, dziekuje bardzo !

Bizon: − Sposób z Δ łatwiejszy?

Anka: a jesli mogłbys Bizon, mi to z deltą jeszcze pokazać rozwiązanie

Bizon: przecież Ci napisałem

Anka: Jeju, nie zauwazyłam, przepraszam Bizon

Bizon: zrozumiałaś? −

Anka: tak, przeanalaizowałam i delta okazałą sie łatwiejsza, gdyz sama tak na początku próbowałam robic, choć nie wiedziałam , czy dobrze.

Anka: Tak, zrozumiałam Jeszcze raz dziękuję za poświecenie mi czasu. Miłego wieczoru !

Bizon: −