Planimetria Sylwia: Ramię AD trapezu ABCD (w którym AB||CD) przedłużono do punktu E takiego, że |AE| = 2 x |AD|. Punkt M leży na podstawie AB oraz ^|AM|_|MB| = 2. Odcinek ME przecina przekątną BD w punkcie P. Udowodnij, że |BP| = |PD|.

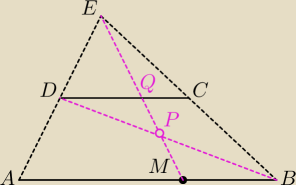
Bizon: Jeśli |AB| oznaczysz jako x to |AM|=2x/3

|AM|		|AM|
	=2 ⇒ |DQ|=		=x/3
|DQ|		2

zauważ, że MB to też x/3 ... i chyba wszystko jasne −