znajdź funkcje odwrotną do funkcji danej wzorem: marta: znajdź funkcje odwrotną do funkcji danej wzorem: f(x)=x/4 + 4/x

Bogdan:

	x		4
y =		+		/*4x dla x≠0 (niebieski wykres)
	4		x

x² − 4yx + 16 = 0, Δ = ..., x = ... lub x = ... (zielony wykres)

Pudel:

	x		4
Zasadniczo funkcja f(x)=		+		nie jest jednowartościowa w całej dziedzinie (w której
	4		x

jest określona) Zatem funkcja odwrotna do niej nie istnieje.Natomiast w pewnych przedziałach... Ale to już jest treścią zadania ;Ustal przedziały odwracalności danej funkcji f(x) i podaj wzory funkcji odwrotnych do danej!

PW:

a

4

b

4

a−b

a−b

(a−b)

16

+

−(

+

) =

− 4

=

(1−

)

4

a

4

b

4

ab

4

ab

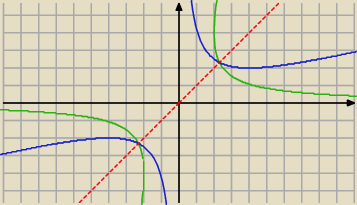
Badamy w ten sposób, czy istnieją liczby a i b, dla których f(a) = f(b). Okazuje się, że różnych a i b jest nieskończenie wiele, są to a i b, dla których ab=16, a≠b. Na przykład f(2)=f(8):

	4		2		4		8
f(2) =		+		= 2,5 i f(8) =		+		= 2,5
	2		4		8		4

Powiedzmy więc jasno: zadanie jest "podpuchą", nie istnieje funkcja odwrotna do f − z prostej przyczyny, że f nie jest różnowartościowa. Piszę to tylko dlatego, że Pudel użył sformułowania "jednowartościowa" i nie udowodnił swojego spostrzeżenia. Sformułował natomiast inne, ciekawe zadanie wybiegające poza to, o które pytała marta