wykres funkcji f której dziedziną jest przedział <-7,7>
:( )::
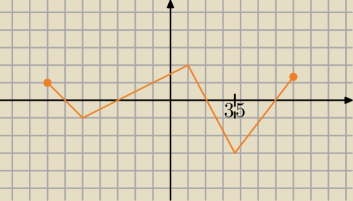
Rysunek przedstawia wykres funkcji f której dziedziną jest przedział <−7,7>.
a)Na podstawie rysunku podaj zbiór rozwiązań nierówności f(x)<0
b)Określ, dla jakiej liczby a prosta o równaniu y=a, gdzie a∊R ma jeden punkt wspólny z
wykresem funkcji f
Tak więc podpunkt "a" wydaje mi się że jest to zbiór {−7,−6,−5,−4,−3,−2,−1}. Ale pewna nie
jestem za to podpunkt "b" w ogóle nie rozumiem
2 lut 12:30
Marcin: Co dla Ciebie oznacza f(x)<0?
2 lut 12:33
:( ): Podstawiam za f(x)<0
f(−7)<0 i tak do tego doszłam xD
2 lut 12:35
Marcin: A czy w Twoim przypadku f(−7) dale liczbę mniejszą od 0?
2 lut 12:36
:( ): :( No bo liczby z minusem są mniejsze od zera ?
2 lut 12:37
Marcin: Ale (−7) to argument. Wyniki masz na 'Igrekach'
rozumiesz?
2 lut 12:42
:( ): Czyli f(7)<0 ?
2 lut 12:45
Marcin: Nie. f(−7)>0, tak samo f(7) Zauważ, że ja po prostu patrzę czy dla danego argumentu wartość
jest nad osią OX lub pod nią.
Dla przykładu
f(−5)=−1 lub f(3.5)=−3 ale za to f(1)=2
2 lut 12:48
:( ): Jeśli cię dobrze zrozumiałam to chodzi co o to ?
f(−7)=1
f(7)=1,4
Bo jak to nie to to już nie wiem
2 lut 12:52
Marcin: Tak. Dobrze mnie rozumiesz
czyli teraz kiedy f(x)<0 (podaj przedziały)
2 lut 12:57
:( ): <−7,−6) u (−3,2) u (6,7> To o to chodzi ?
2 lut 13:04
:( ): A chyba nie dla f(x) < 0
Jeśli 0 jest większe to chyba to bd to:
<−6;−3) u (2;6>
2 lut 13:07
Marcin: Akurat teraz podałaś f(x)>0
2 lut 13:08
Marcin: Wszystko teraz jest ładnie, ale musisz pamiętać, że jak masz ostro większe/mniejsze od np 0, to
przedziały są otwarte
2 lut 13:09
:( ): <−7,−6) u (−3,2) u (6,7> czyli to jest dobrze xD ?
2 lut 13:09
Marcin: (−6;−3) ∪ (2;4)
2 lut 13:12
Marcin: (−6;−3) ∪ (2;6) Poprawiam się
2 lut 13:12
:( ): OK
Przepraszam troszkę się zmieszałam i nie wiedziałam już które
a z podpunktem "b" pomożesz ?
2 lut 13:13
Marcin: Według mnie będzie tak dla dwóch takich liczb a, a teraz pomyśl jak wygląda prosta y=2
2 lut 13:18
:( ): maleje w przedziale (2,−3)
2 lut 13:20
:( ): zauważyłam że przecina się z osią x w punkcie 2
2 lut 13:23
Marcin: Prosta y=2 nie maleje. Jest stała.
2 lut 13:29
2 lut 13:30
:( ): y=2 dla x =1 ?
2 lut 13:34
Marcin: Dla dowolnego X, y=2
W przypadku tej prostej oczywiście.
2 lut 13:35
:( ): No tak ale nadal nie rozumiem i nie wiem jak wywnioskować odpowiedz do podpunktu b
2 lut 13:37
Marcin:
2 lut 13:40
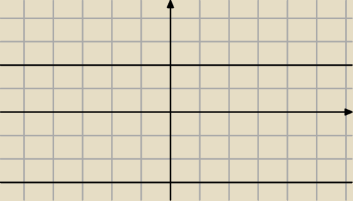
Marcin: Tutaj masz narysowane dwie proste. y=2 i y=−3 Nanieś teraz na to swój wykres i zobaczysz, że
dla tych prostych masz jeden punkt wspólny z Twoim wykresem.
2 lut 13:41
:( ): Patrząc na funkcję znajdują się na tych liniach dwa punkty
2 lut 13:42
Marcin: Ale rozważ to osobno. W sensie dla jednej prostej, a później dla drugiej
Wtedy każda z
prostych ma jeden punkt wspólny z Twoim wykresem.
2 lut 13:44
:( ): Dzięki że się ty tak ze mną pomęczyłeś
2 lut 13:45
Marcin: No problem. Sam się uczę
2 lut 13:46
:( ): Myślałam że jestes nauczycielem xD Tak fajnie tłumaczysz
2 lut 13:49
Marcin: Tak, tak. Nauczycielem, który w tym roku pisze maturę
2 lut 13:53
:( ): Haha .. młodo zacząłeś xD
2 lut 13:55